Пусть ф.  на
на  задана табл.
задана табл.  с равноотстоящими узлами
с равноотстоящими узлами  . К_Р
. К_Р  порядка k опред. рекуррентно через К_Р порядка k-1равенством
порядка k опред. рекуррентно через К_Р порядка k-1равенством  (1). Здесь К_Р нулевого порядка берутся равными знач.
(1). Здесь К_Р нулевого порядка берутся равными знач.  ф. в узлах.
ф. в узлах.
Лемма. РР в случае равноотстоящих узлов выраж. через К_Р по форм.  (2).
(2).
В случае выбора в качестве узлов интерпол. табл. узлов  формула Ньютона с Раздел.Р принимает вид
формула Ньютона с Раздел.Р принимает вид  (3)
(3)
Заменим в ней РР конечн. в соотв. с (2). Получим
 (4). В форм. (4) сделаем замену переменной по правилу
(4). В форм. (4) сделаем замену переменной по правилу  (4′). Форм. (4′) наз интерпол. форм. Ньютона для интерпол. в начале таблицы или для интерпол. вперед. Здесь имеется в виду, что при p = 0 первый узел интерпол. совп. с нач. узлом табл. и остал. интерпол. узлы распред. от него вниз (вперед) по таблице. В качестве узлов интерпол. возьмем теперь табл. узлы
(4′). Форм. (4′) наз интерпол. форм. Ньютона для интерпол. в начале таблицы или для интерпол. вперед. Здесь имеется в виду, что при p = 0 первый узел интерпол. совп. с нач. узлом табл. и остал. интерпол. узлы распред. от него вниз (вперед) по таблице. В качестве узлов интерпол. возьмем теперь табл. узлы  . Так. инт. форм. Ньютона с РР примет вид
. Так. инт. форм. Ньютона с РР примет вид  . (5) Т. к. РР явл. симметр. ф. своих аргументов, то по форм. (2) имеем
. (5) Т. к. РР явл. симметр. ф. своих аргументов, то по форм. (2) имеем  . (6)
. (6)
Заменим в форм. (5) РР конечн. в соотв. с форм. (6). Получим  .(7)
.(7)
В форм. (7) сделаем замену перемен. по правилу  :
:  (7′)
(7′)
Форм. (7′) наз. инт. формулой Ньютона для инт-ия в конце табл. или для инт-ия назад. Здесь имеется в виду, что при  первый узел инт-ии совпадает с последним узлом таблицы и остальные инт-ые узлы распол. от него вверх (назад) по таблице.
первый узел инт-ии совпадает с последним узлом таблицы и остальные инт-ые узлы распол. от него вверх (назад) по таблице.
Зам. В кач. нач. узла инт-ии обычно выбир. табл. узел  , ближайший к зад. знач. аргумента x. Далее выч.
, ближайший к зад. знач. аргумента x. Далее выч.  . Если
. Если  , в качестве инт-ых берутся табл. узлы вниз от
, в качестве инт-ых берутся табл. узлы вниз от  и выч. провтор. по инт. форм. Ньютона (4′) для инт. в начале табл. В случ. когда
и выч. провтор. по инт. форм. Ньютона (4′) для инт. в начале табл. В случ. когда  , в качестве инт. берутся табл. узлы вверх от
, в качестве инт. берутся табл. узлы вверх от  и вычисления проводятся по инт. формуле Ньютона (7′) для инт-ия в конце табл.
и вычисления проводятся по инт. формуле Ньютона (7′) для инт-ия в конце табл.
Составление таблиц.
Для заданной ф.  требуется постр. на
требуется постр. на  табл.
табл.  . При этом постоянный шаг табл. h должен быть выбран так, чтобы таблица допускала инт-ию многочл. степени k с задан. точностью
. При этом постоянный шаг табл. h должен быть выбран так, чтобы таблица допускала инт-ию многочл. степени k с задан. точностью  . При решении поставленной задачи воспольз. полученной оценкой остаточн. члена ИМ Лагранжа степени k по узлам
. При решении поставленной задачи воспольз. полученной оценкой остаточн. члена ИМ Лагранжа степени k по узлам  :
:  , (1) где
, (1) где  ,
,  . Т. о., шаг табл. h следует выбрать так, чтобы удовл. нерав.
. Т. о., шаг табл. h следует выбрать так, чтобы удовл. нерав.  .(2) Проведем замену переменного по прав.
.(2) Проведем замену переменного по прав.  . Такое нерав. (2) принимает вид
. Такое нерав. (2) принимает вид  . Следов., искомое знач. шага табл. h должно удовл. нерав.
. Следов., искомое знач. шага табл. h должно удовл. нерав.  (3). Здесь предпол., что знач. аргум. x
(3). Здесь предпол., что знач. аргум. x  отрезку инт-ии
отрезку инт-ии  . Итак, задача нахожд. искомого знач. шага табл. h сводится к задаче нахождения max ф.
. Итак, задача нахожд. искомого знач. шага табл. h сводится к задаче нахождения max ф.  на отрезке
на отрезке  .В случае линейной инт-ии k=1 имеем
.В случае линейной инт-ии k=1 имеем  . Решение ур.
. Решение ур.  дает
дает  . Т.о., табл. допускает линейную инт-ию с заданной точн., если ее шаг удовл. нерав.
. Т.о., табл. допускает линейную инт-ию с заданной точн., если ее шаг удовл. нерав.  . (4)
. (4)
Для ф.  имеем
имеем  и при
и при  можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем
можно взять h=0.002. В случае квадратичной интерполяции k= 2имеем  . Решение ур.
. Решение ур.  дает
дает  .Получаем
.Получаем
 . Т.о., табл. допускает квадратичную инт-ю с заданной точностью, если ее шаг удовл. нерав.
. Т.о., табл. допускает квадратичную инт-ю с заданной точностью, если ее шаг удовл. нерав.  (5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы табл. узел
(5) Если при квадр-ой инт-ии выбирать узлы инт-ии так, чтобы табл. узел  был ближайшим к x,то будет выполн. нерав.
был ближайшим к x,то будет выполн. нерав.  или
или  и при выборе шага нужно находить только
и при выборе шага нужно находить только  . Поскольку
. Поскольку  , то ф.
, то ф. 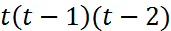 на
на  монотонно убывает. Следов.,
монотонно убывает. Следов.,  . В резул. приходим к оценке шага табл.
. В резул. приходим к оценке шага табл.  .(6) Для ф.
.(6) Для ф.  имеем
имеем  и при
и при  можно взять h= 0.02.Табл. ф. y=sin x, дополн. кв-ую инт-ию, требует для своего хранен. в 10 раз < объема памяти, чем табл. этой же ф., дополн. только лин-ую инт-ию.
можно взять h= 0.02.Табл. ф. y=sin x, дополн. кв-ую инт-ию, требует для своего хранен. в 10 раз < объема памяти, чем табл. этой же ф., дополн. только лин-ую инт-ию.






