Определение .Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
Пример 18. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть 
– число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины .
m Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.
Таким образом, закон распределения может считаться биноминальным.
?
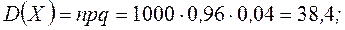Пример 19. Найти дисперсию дискретной случайной величины 
– числа появлений события в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что 
.
m Так как случайная величина распределена по биноминальному закону, то
?
Функция распределения
Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.
Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что примет значение, меньшее х, то есть 
, обозначим через 
.
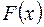Определение. Функцией распределения называют функцию 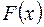, определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее х.
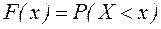
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины разрывна и возрастает скачками при переходе через каждое значение хi.
Пример 20. Задана интегральная функция распределения:
Построить ее график.
m
| |||
| 0,3 | 0,1 | 0,6 |
?
