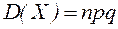1. Математическое ожидание постоянной величины равно самой постоянной.
2. Постоянный множитель можно выносить за знак математического ожидания.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
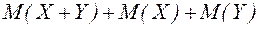
Это свойство также справедливо для произвольного числа случайных величин.
Пусть производится 
независимых испытаний, вероятность появления события 
в которых равна 
.
Теорема. Математическое ожидание 
числа появления события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.
Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
Определение. Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Пример 17. Для рассмотренного выше примера закон распределения случайной величины имеет вид:
| |||
|
| 0,0625 | 0,375 | 0,5625 |
Найти математическое ожидание и дисперсию случайной величины.
m
Математическое ожидание случайной величины равно:
Возможные значения квадрата отклонения:
Тогда
| 2,25 | 0,25 | 0,25 |
|
| 0,0625 | 0,375 | 0,5625 |
Дисперсия равна:
. ?
Однако, на практике подобный способ вычисления дисперсии неудобен, так как приводит при большом количестве значений случайной величины к громоздким вычислениям.
Поэтому применяется другой способ.
Вычисление дисперсии
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Доказательство. С учетом того, что математическое ожидание и квадрат математического ожидания 
– величины постоянные, можно записать:
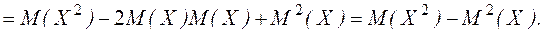
Применим эту формулу для рассмотренного выше примера:
|
| |||
| |||
|
| 0,0625 | 0,375 | 0,5625 |
Свойства дисперсии
1. Дисперсия постоянной величины равна нулю.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события в независимых испытаний, в каждом из которых вероятность появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.
