1. Плотность распределения – неотрицательная функция.
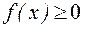
2. Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.
Пример 22. Случайная величина подчинена закону распределения с плотностью:
Требуется найти коэффициент а, определить вероятность того, что случайная величина попадет в интервал от 0 до 
.
m
1) Для нахождения коэффициента а воспользуемся свойством 
.
2) Находим вероятность попадания случайной величины в заданный интервал. 
. ?
Числовые характеристики непрерывных случайных величин
Пусть непрерывная случайная величина 
задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [ a,b ].
Определение. Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
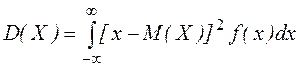
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.
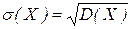
Пример 23. Случайная величина 
задана интегральной функцией распределения 
.
Найти:
1) дифференциальную функцию (плотность вероятностей);
2) математическое ожидание.
m
. ?
Законы распределения непрерывных случайных величин
При решении практических задач зачастую точно найти закон распределения случайной величины довольно сложно. Однако, все происходящие процессы, связанные со случайными величинами, можно разделить на несколько типов, каждому из которых можно поставить в соответствие какой – либо закон распределения.
Выше были рассмотрены некоторые типы распределений дискретной случайной величины такие как биноминальное распределение и распределение Пуассона.
Рассмотрим теперь некоторые типы законов распределения для непрерывной случайной величины.
Равномерное распределение
Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [ a, b ], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.
Постоянная величина 
может быть определена из условия равенства единице площади, ограниченной кривой распределения.
Получаем 
.
f(x) 
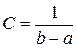
0 a b x
Найдем функцию распределения F(x) на отрезке [ a,b ].
F(x)
0 a b x
Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.
Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.
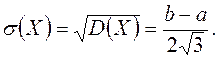
Вероятность попадания случайной величины в заданный интервал:
Пример 24. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого значения. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04, б) большая 0,05.
m 
а)
Ответ: 
б)
Ответ: 
?
Пример 25. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ждать автобус менее 3 минут.
m 
Ответ: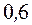 
?
