Пусть некоторое событие 
может произойти вместе с одним из несовместных событий 
, составляющих полную группу событий. Пусть известны вероятности этих событий 
и условные вероятности наступления события при наступлении события 
:
.
Теорема. Вероятность события , которое может произойти вместе с одним из событий , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события .
Пример 5. В двух ящиках содержатся по 20 деталей, причем в первом 17 стандартных деталей, а во втором 15 стандартных деталей. Из второго ящика наудачу извлечена одна деталь и переложена в первый ящик. Найти вероятность того, что наудачу извлеченная деталь из первого ящика, окажется стандартной.
¦ Опыт можно разбить на два этапа: первый - перекладывание детали,
второй - выбор детали.
Гипотезы:
- переложена стандартная деталь;
- переложена нестандартная деталь.
, 
.
, 
.
. ?
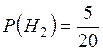Пример 6. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.
m
Вероятность того, что выстрелы производит первый, второй или третий стрелок равна 
.
Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: 
- для второго стрелка: 
- для третьего стрелка: 
Искомая вероятность равна:
. ?
Формула Байеса (формула гипотез)
Пусть имеется полная группа несовместных гипотез с известными вероятностями их наступления . Пусть в результате опыта наступило событие , условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности .
Требуется определить какие вероятности имеют гипотезы относительно события , то есть условные вероятности 
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Эта формула называется формулой Байеса.
.
Пример 7. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру равна 0,6, ко второму равна 0,4. Вероятность того, что деталь будет признана стандартной первым контролером равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что ее проверил первый контролер.
¦ Гипотезы: - деталь проверил первый контролер;
- деталь проверил второй контролер.
Событие 
- деталь признана стандартной.
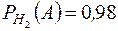
Как видно до испытания , а после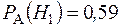 
. ?
Повторение испытаний
Формула Бернулли
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие , и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события .
Допустим, что событие наступает в каждом испытании с вероятностью 
. Определим вероятность 
того, что в результате 
испытаний событие наступило ровно 
раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям.
Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
Пусть в результате независимых испытаний, проведенных в одинаковых условиях, событие наступает с вероятностью , а противоположное ему событие 
с вероятностью 
.
Обозначим 
– наступление события в испытании с номером 
. Так как условия проведения опытов одинаковые, то эти вероятности равны.
Если в результате опытов событие наступает ровно раз, то остальные 
раз это событие не наступает. Событие может появиться раз в испытаниях в различных комбинациях, число которых равно количеству сочетаний из элементов по . Это количество сочетаний находится по формуле:
Вероятность каждой комбинации равна произведению вероятностей:
Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:
Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, то есть того самого случая, в котором наиболее четко проявляются законы теории вероятностей.
Пример 8. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
m
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
Так как выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в 
испытаниях событие в вероятностью 
наступает ровно раз.
В случае пяти попаданий из пяти возможных:
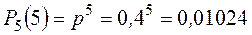
Четыре попадания из пяти выстрелов:
Три попадания из пяти:
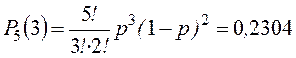
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
. ?
