Нормальный закон распределения

Определение.Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

,

где ,

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины .

Найдем функцию распределения .

,

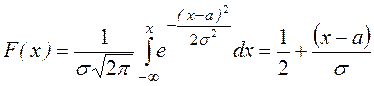где ,

График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1. Функция определена на всей числовой оси.

2. При всех х функция распределения принимает только положительные значения.

3. Ось является горизонтальной асимптотой графика плотности вероятности, так как при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.

4. Найдем экстремум функции.

Так как при y’ > 0 при x <а и y’ < 0 при x > а , то в точке х = а функция имеет максимум, равный .

5. Функция является симметричной относительно прямой х = а, так как разность (х – а) входит в функцию плотности распределения в квадрате.

6. Для нахождения точек перегиба графика найдем вторую производную функции плотности.

При x = а+ s и x = а - s вторая производная равна нулю, а при переходе через эти точки меняет знак, то есть в этих точках функция имеет перегиб.

В этих точках значение функции равно .

Построим график функции плотности распределения.

Графики при различных значениях и имеют вид:

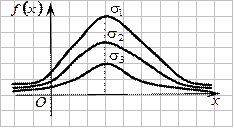
Параметр характеризует положение кривой, а параметр - форму кривой нормального распределения.

При распределение называется стандартным нормальным, а график называется нормированной кривой.

.

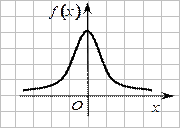
Если случайная величина распределена по нормальному закону, то

Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания по модулю меньше заданного числа равна .

Правило трех

Если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

.

На практике это правило используют так: если распределение случайной величины не известно, но правило трех выполняется, то есть основание предполагать, что случайная величина распределена нормально.

Нормальному закону распределения подчиняются ошибки измерений, величины износа деталей в механизмах, рост человека, колебание курса акций и т.д.

Пример 27.Случайна величина распределена по нормальному закону , а вероятность ее попадания в интервал равна 0,8. Найти вероятность попадания в интервал .

¦

; ;

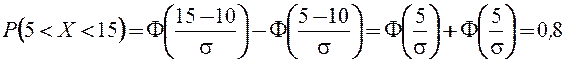
l

Дата добавления: 2016-03-27; просмотров: 221 | Нарушение авторских прав