1. 
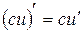де 
.
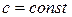2. 
.
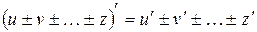3. (uv)’ =u'v + uv'.
Останнє правило поширюється на добуток п співмножників: похідна добутку п функції дорівнює добутку похідної першого співмножника на всі інші плюс добуток похідної другого співмножника на всі інші плюс і т.д., плюс добуток похідної п -го співмножника на всі інші:
4. 
; 
.
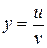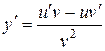Похідна складної функції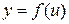 
, де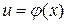 
, тобто 
, дорівнює добутку похідної даної функції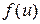 
по проміжному аргументу 
на похідну проміжного аргументу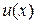 
по 
:
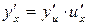(2.13)
Аналогічне правило має місце й у випадку, коли складна функція задана ланцюжком, що містить три і більш ланки. Наприклад, якщ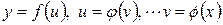о 
, то:
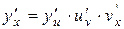(2.14)
Приклад 2.35. Знайти похідну функції 
.
Розв’язання. Спочатку знаходимо похідну від логарифму, враховуючи, що проміжним аргументом є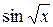 
. Отримуємо 
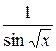. Подумки закреслюємо вираз 
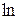та бачимо вираз 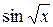. Диференціюємо синус (проміжним аргументом в даному випадку є 
). Отримуємо 
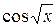. Подумки закреслюємо вираз 
, та бачимо вираз . Диференціюємо корінь: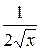 
. Залишається х, похідна від якого дорівнюється одиниці. Тепер 
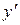запишемо у вигляді добутку всіх проміжних результатів:
Для правильного вибору першої (основної) функції рекомендуємо таке правило: нею буде та функція, яка виконується останньою (виключення складає показникова функція).
Приклад 2.36. Знайти похідну функції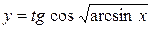 
.
Розв’язання. За формулою (2.14) та використовуючи таблицю основних формул диференціювання маємо:
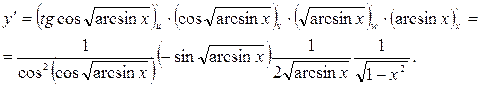
Рекомендуємо для зменшення громіздких записів наступний прийом, що дає можливість проводити роздроблення складної функції на ланки усно і записати вираз для похідної відразу.
Приклад 2.37. Знайти похідну функції: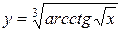 
.
Розв’язання. подумки виконуємо диференціювання спочатку 
, потім 
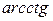, та 
.
результат: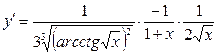 
.
Зауваження 1. Варто пам'ятати, що на кожній стадії диференціюється тільки один вид функції. Так, диференціюючи функцію 
, ми спочатку диференціюємо тільки корінь кубічний, а потім лише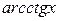 
.
Типова помилка полягає в тому, що відразу диференціюють кілька функцій 
(невірний результат).
Зауваження 2. Зустрічаються функції, які доцільно спочатку спростити, а потім диференціювати. Так, якщо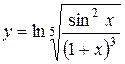 
, то після того, як ми функцію логарифмуємо та запишемо у вигляді 
, диференціювання істотно спроститься.
Приклад 2.38. Знайти рівняння дотичної і нормалі до параболи
у точці, де х = 2.
Розв’язання. Відповідно до геометричного змісту похідна функції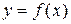 
в точці 
дорівнює тангенсу кута нахилу дотичної до графіка функції в цій точці. Рівняння дотичної до кривої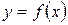 
у точці М(х0,у0):
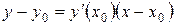(2.15)
Перпендикуляр АВ до дотичної в точці М називається нормаллю до кривої в цій точці. З огляду на умову перпендикулярності прямих (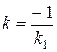
), рівняння нормалі запишеться у виді:
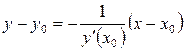(2.16).
Абсцисі х = 2 відповідають ординати 
, так що треба знайти рівняння дотичної і нормалі в точці М(2, 0). Знаходимо у'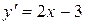 
. У точці М(2, 0) у'= 1.
За формулою (2.15) рівняння дотичної має наступний вид у точці М: 
.
Рівняння нормалі у точці А знайдемо за формулою (2.16):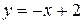 
.
Контрольний тест. Знайти похідні функцій:
| Функція | Похідна | Функція | Похідна |
1. 
| 
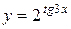
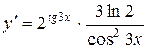
| 2.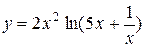 
| 
|
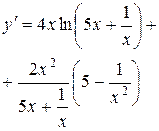
3. 
| 
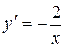
| 4.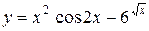 
| 
|
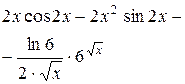
5. 
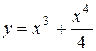при х =1
| 6.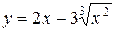 
при х =1
|
