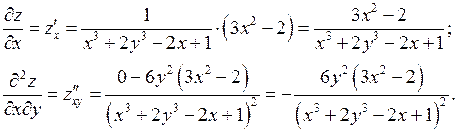Схема дослідження функції.
1. Знайти область визначення функції.
2. Знайти точки розриву (якщо вони є) та визначити їх вид.
3. Визначити асимптоти графіка функції.
4. Визначити парність, непарність і тим самим симетричність графіка функції.
5. Знайти точки екстремуму, інтервали монотонності.
6. Знайти точки перегину, інтервали опуклості й угнутості графіка функції.
7. За отриманими даними побудувати графік функції. Для уточнення графіка функції іноді корисно визначити точки перетину графіка з осями координат.
Приклад 2.54. Провести повне дослідження функції 
та побудувати її графік.
Розв’язання.
1) Знайдемо область визначення функції: 
.
2) Функція неперервна на всій осі як елементарна.
3) У графіка цієї функції відсутні асимптоти. Якщо функція неперервна, то відсутні вертикальні асимптоти. При знаходженні похилих асимптот 
параметр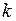 
не дорівнює скінченному числу:
.
4) Функція не є ні парною, ні непарною:
5) Знайдемо інтервали монотонності та критичні точки функції за допомогою першої похідної.
.
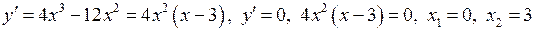Одержані точки розбивають область визначення функції на такі інтервали: 
. Знайдемо знак похідної в кожному з інтервалів.
6) Знайдемо інтервали угнутості та точки перегину графіка функції за допомогою похідної другого порядку.
.
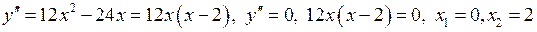Критичні точки другого порядку 
розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.
.
Точки перегину функції мають координати: 
і 
.
7) Знайдемо точки перетину функції з осями координат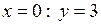: при 
; при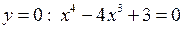 
. Для рівняння 
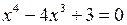можна методом підбору знайти один корінь 
.
Побудуємо схематично графік функції (рис. 2.12).
Рис. 2.12
Приклад 2.54. Провести повне дослідження функції 
та побудувати її графік.
Розв’язання. 1) Знайдемо область визначення функції. Необхідно знайти ті точки, в яких знаменник дробу дорівнює нулю і виключити їх. Одержимо 
. Функція визначена в інтервалах 
.
2) Точки розриву другого роду:
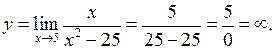
3) Знайдемо асимптоти графіка функції.
а) Вертикальні асимптоти будемо шукати в точках розриву функції. Одержимо:
прямі 
та 
є вертикальними асимптотами функції.
б) Похилі асимптоти будемо шукати у вигляді , а невідомі параметри 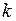і 
визначимо за формулами (2.23). Одержимо
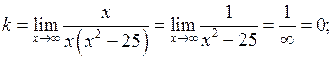
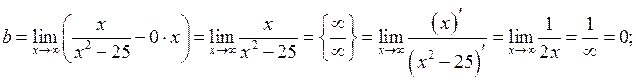
, тоді 
– вісь 
– горизонтальна асимптота.
4) Для функції виконується умова
.
Функція непарна, а її графік центрально-симетричний відносно початку координат.
5) Знайдемо інтервали монотонності та критичні точки функції. Для цього знайдемо першу похідну функції. Маємо:
;
.
Тоді 
для всіх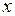 
із області неперервності.
Тобто функція спадна на кожному інтервалі області визначення.
6) Знайдемо інтервали вгнутості та точки перегину графіка функції. Для цього знайдемо другу похідну.
Прирівняємо 
. Одержимо 
; 
– критична точка.
Знайдемо знак другої похідної в кожному з інтервалів 
.
Маємо 
.
На інтервалах 
та 
графік опуклий, а на інтервалах 
та 
– вгнутий. Точка 
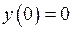є точкою перегину графіка функції.
7) Знайдемо точки перетину графіка функції з осями координат: при 
, при 
. Інших точок не існує.
Використовуючи результати досліджень, побудуємо графік функції (рис. 2.13).
|
|
Рис. 2.13
Побудуємо графік функції. Графік перетинає осі координат у точці О(0;0).
Найбільше і найменше значення функції на відрізку
Нехай функція 
неперервна на відрізку 
. Як відомо, така функція досягає своїх найбільшого і найменшого значень. Ці значення функція може приймати або у внутрішній точці 
відрізка , або награниці відрізка, тобто при 
або 
.Якщо 
, то її слід шукати серед критичних точок даної функції (див. рис. 2.14).
Рис. 2.14
Одержуємо наступне правило знаходження найбільшого і найменшого значень функції на :
1) знайти критичні точки функції на інтервалі 
;
2) обчислити значення функції в знайдених критичних точках;
3) обчислити значення функції на кінцях відрізку, тобто при або ;
4) серед всіх обчислених значень функції вибрати найбільше і найменше.
Зауваження: 1. Якщо функція на відрізку маєлише одну критичну точку і вона є точкою максимуму (мінімуму), то в цій точці функція приймає найбільше (найменше) значення. На рисунку 6 
і 
2. Якщо функція на відрізку не має критичних точок, то це означає, що на ньому функція монотонно зростає або спадає. Отже, своє найбільше значення функціяприймає на одному кінці відрізка, а найменше — на іншому.
Приклад 2.55. Знайти найбільше та найменше значення функції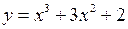 
на відрізку 
.
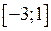Розв’язання. Функція може досягати свого найбільшого та найменшого значення або на кінцях відрізка, або у критичних точках, якщо вони знаходяться у середині відрізка. Знайдемо критичні точки функції і розглянемо тільки ті, які потрапляють в інтервал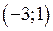 
.
.
Обчислимо значення функції у критичних точках та на кінцях відрізка. Одержимо:
;
;
; 
.
Відповідь. 
– найбільше значення функції; 
– найменше значення функції на відрізку.
ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
8.1 Частинні похідні і повний диференціал
Функцією двох змінни х називається правило (відповідність), по якому кожній парі чисел 
відповідає єдине число 
. Множина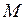 
– область визначення функції, а 
– множина значень функції.
Для функцій двох та багатьох змінних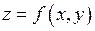 
, 
розглянемо частинні похідні.
Частинною похідною функції 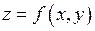по одній змінній називають скінченну границю виду:
де 
та 
– частинний приріст функції по одній змінній.
Повним диференціалом функції багатьох змінних називається головна лінійна частина приросту функції. Для функції 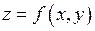повний диференціал має вигляд
.
Повний диференціал функції багатьох змінних застосовується до наближених обчислень, вважаючи, що 
.
Частинні похідні знаходяться за правилами та формулами диференціювання функції однієї змінної, вважаючи решту змінних сталими величинами.
Частинною похідною n-го порядку функції багатьох змінних по одній змінній називають першу похідну від 
-ї похідної.
Приклад 2.56. Знайти частинні похідні другого порядку функції
.
Розв’язання. Знайдемо частинні похідні першого порядку по кожній змінній:
Від кожної частинної похідної першого порядку 
та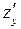 
знайдемо першу похідну по кожній змінній. Це будуть частинні похідні другого порядку і їх буде чотири:
Мішані похідні, які відрізняються порядком диференціювання, 
, рівні між собою. Ця умова виконується у випадку їх неперервності.
Приклад 2.57. Знайти 
, якщо 
.
Розв’язання. Знайдемо частинну похідну функції тільки по 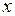або по 
, а потім від неї знайдемо першу похідну по іншій змінній. Одержимо
