Розглянемо задачу про продуктивність праці. Нехай функція и = и(t) відображає кількість виробленої продукції u за час t i необхідно знайти продуктивність праці в момент t0.
За період часу від t 0 до t 0 +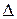 
t кількість виробленої продукції зміниться від значення u 0 = u(t 0 ) до значення u 0 + 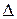u = u(t 0 + 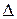t); тоді середня продуктивність праці за цей період часу zсер= 
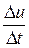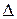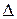. Очевидно, що продуктивність праці в момент t 0 можна визначити як граничне значення середньої продуктивності за період часу від t 0 до t 0 + t при t à 0, тобто
Таким чином, продуктивність праці є похідна від обсягу виробленої продукції по часу.
Розглянемо ще одне поняття, яке ілюструє економічний зміст похідної.
Витрати виробництва y будемо розглядати як функцію кількості продукції х, що виробляється. Нехай 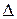х — приріст продукції, тоді 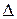y — приріст витрат виробництва і 
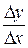– середній приріст витрат виробництва продукції на одиницю продукції. Похідна у' = 
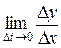виражає граничні витрати виробництва і характеризує наближено додаткові затрати на виробництво одиниці додаткової продукції.
Граничні витрати залежать від рівня виробництва (кількість продукції, що випускається) і визначаються не постійними виробничими затратами, а лише змінними (на сировину, паливо та ін.). Аналогічним чином можуть бути визначені гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.
Застосування диференціального числення для дослідження економічних об'єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об'єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об'єкта (процесу) за часом або відносно іншого об'єкта дослідження. Але необхідно врахувати, що економіка не завжди дозволяє використовувати граничні величини в силу неподільності багатьох об'єктів економічних розрахунків та перервності (дискретності) економічних показників в часі (наприклад, річних, квартальних, місячних та ін.). Водночас у деяких випадках можна відокремитись від дискретності показників і ефективно використовувати граничні величини.
Означення похідної
Нехай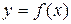 
– деяка функція, задана на інтервалі (а,b). Візьмемо довільну точку 
з цього інтервалу. Обчислимо значення функції в цій точці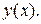 
Додамо аргументу приріст 
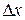такий, що точка 
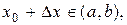й обчислимо нове значення функції 
.
|
.
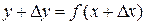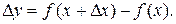
Якщо існує границя відношення 
при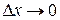 
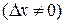, то ця границя називається похідною функції 
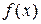в точці і позначається 
або 
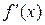або 
або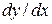 
— (читається: де ігрек по де ікс).
(2.12)
| обчислення похідної називають диференціюванням. Якщо похідна функції 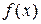в точці існує, то функція називається диференційовноюу точці . Якщо функція диференційована в кожній точці деякого проміжку, то вона називається диференційованою на цьому проміжку.
|
Поняття похідної дозволяє характеризувати поведінку функції.
