При обчисленні границі функції 
приходиться зустрічатися з двома різними типами прикладів.
· Функція визначена в граничній точці х = а. Тоді 
.
Приклад 2.3. Знайти границю 
.
Розв’язання. Для обчислення границіфункції 
заміняємо змінну х її граничним значенням, тобто
.
· Функція в граничній точці х = а не визначена або обчислюється границя функції при 
. Тоді обчислення границі в кожному випадку вимагає індивідуального підходу. В одних задачах питання зводиться безпосередньо до застосування теорем про властивості нескінченно малих, в інших – функція 
в точці х = а або при являє собою невизначеність, тобто вираз виду 
, та інші.
Невизначеність 
розкривають винесенням аргументу з найбільшим показником степені з чисельника і знаменника дробу і скороченням на нього.
Приклад 2.4. Знайти границю 
.
Розв’язання. У чисельнику і знаменнику дробу винесемо за дужки 
і скоротимо на нього:
.
Приклад 2.5. Знайти границю 
.
Розв’язання. У чисельнику і знаменнику дробу винесемо за дужки і скоротимо на нього:
Приклад 2.6. Знайти границю 
.
Розв’язання. У чисельнику і знаменнику дробу винесемо за дужки 
і скоротимо на нього:
.
З прикладів видно, що при розкритті невизначеності , породжуваної відношенням двох многочленів, можна скористатися наступним правилом:
· якщо показник старшого степеня чисельника більше показника старшого степеня знаменника, то границя дробу дорівнює нескінченності;
· якщо показник старшого степеня чисельника дорівнює показнику старшого степеня знаменника, то границя дробу дорівнює відношенню коефіцієнтів при показниках старших степенів;
· якщо показник старшого степеня чисельника менше показника старшого степеня знаменника, границя дробу дорівнює нулю.
Приклад 2.7. Знайти границю 
.
Розв’язання. Показник старшого степеня чисельника 4/3, а знаменника – 2. За вищевказаним правилом маємо: =0.
Приклад 2.8. Знайти границю 
.
Розв’язання. Показник старшого степеня чисельника 2, знаменника також 2. За вищевказаним правилом маємо:
Приклад 2.9. Знайти границю 
.
Розв’язання. Показник старшого степеня чисельника 3, знаменника 2. За вищевказаним правилом маємо: 
Невизначеність {¥ – ¥} розкривають в залежності від виду функції. Якщо хоч один член різниці ірраціональний, то розкривають невизначеність помноживши і поділивши вираз, що знаходиться під знаком границі, на спряжений вираз, позбуваючись від ірраціональності в чисельнику. Якщо функція –різниця дробів, то позбуваються невизначеності приведенням дробів до спільного знаменника.
Приклад 2.10. Знайти границю 
.
Розв’язання. Помножимо і поділимо вираз, що стоїть під знаком границі, на спряжений вираз виду 
:
Приклад 2.11. Знайти границю 
.
Розв’язання. Приведемо до спільного знаменника дроби, тоді
.
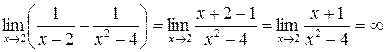Невизначеність 
розкривають виділенням у чисельнику і знаменнику множника, який дорівнює нулю (критичного множника) і скороченням на нього, або позбавленням від ірраціональності.
Приклад 2.12. Знайти границю
.
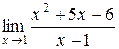Розв’язання. При х =1 чисельник та знаменник дорівнюють нулю, тому це невизначеність виду .Виділимо в чисельнику критичний множник і скоротимо на нього
.
Приклад 2.13. Знайти границю 
.
Розв’язання. У цьому прикладі при х = 1 чисельник і знаменник дробу дорівнюють нулю, це невизначеність . Розділимо многочлени, що знаходяться у чисельнику та знаменнику, на “критичний множник” 
. Після додаткових перетворень, одержимо
.
Приклад 2.14. Знайти границю 
.
Розв’язання. 
.Для розкриття невизначеності виду в цьому випадку чисельник і знаменник треба розкласти на множники і скоротити на спільний множник.
Приклад 2.15. Знайти границю
.
Розв’язання. при х = 0 чисельник і знаменник дробу дорівнюють нулю, це невизначеність .Позбудемося від ірраціональності в чисельнику, розклавши знаменник дробу на множники:
.
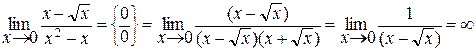Приклад 2.16. Знайти границю 
.
Розв’язання. При х = 1 чисельник і знаменник дробу дорівнюють нулю, це невизначеність . Позбудемося від ірраціональності в чисельнику і знаменнику, шляхом множення чисельника і знаменника дробу на відповідні спряжені вирази:
.
