| Якщо функція у і аргумент х пов'язані рівнянням f(x,y) = 0, нерозв’язаним відносно у, то таке рівняння визначає неявну функцію у(х). |
Наприклад, рівняння у3 - х2 =0 неявно визначає функцію 
. Тут можна розв’язати рівняння відносно у, але в багатьох випадках це неможливо (наприклад, 
). Неявна функція - це не новий вид функції, а просто спосіб її задання.
Треба знайти похідну неявної функції, не знаходячи у у явному виді. Для цього диференціюють обидві частини рівняння f(x,y)= 0(або f(x, у)=j(х, у ), враховуючи при цьому, що у є функція від х, і з отриманого співвідношення знаходять у'.
Приклад 2.39. знайти похідну 
від функції заданої неявно 
.
Розв’язання.
Функцію 
задано в неявному виді. Диференціюємо обидві частини рівняння, пам’ятаючи, що є функцією аргументу 
:
Розв’язуємо рівняння відносно у′; 
; 
, 
Приклад 2.40. знайти похідну від функції заданої неявно 
.
Розв’язання.
Диференціюємо обидві частини рівняння і, з огляду на те, що у є функцією від х. Маємо: 
.
Звідси 
; 
.
Приклад 2.41. знайти похідну від функції, заданої неявно 
.
Розв’язання. Диференціюємо, враховуючи, що у є функцією від х. Маємо: 
.
Контрольний тест.
Знайдіть похідні функцій, заданих неявно наступними рівняннями.
| Функція | Відповіді | Функція | Відповіді | ||
| 
| 
| 
| ||
| 
| 
| 
|
Логарифмічне диференціювання
для знаходження похідної від степенево-показникової функції 
, де 
функції диференційовані по х, необхідно спочатку функцію прологарифмувати, а потім продиференціювати, вважаючи у складною функцією. Отримане рівняння розв’язують відносно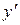 
. Така операція називається логарифмічним диференціюванням.
Приклад 2.41. знайти похідну від функції: 
.
Розв’язання. Це степенево – показникова функція. Логарифмуємо
, 
. Вважаючи неявно заданою функцією, знаходимо похідні лівої та правої частин рівняння. В лівій частині міститься функція ln(y), а в правій - добуток двох функцій, і для його диференціювання потрібно використати формулу похідної добутку 
.
Знайдемо 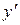, причому записуємо у заданому вигляді
Логарифмічне диференціювання доцільно застосовувати до функції, що містить операції, які логарифмуються: множення, ділення, піднесення до степеня.
Приклад 2.42. знайти похідну від функції:
Розв’язання. Використання звичайних формул і правил диференціювання в даному випадку приведе до громіздких викладок. Тут доцільно застосувати логарифмічне диференціювання. Логарифмуємо обидві частини даної рівності:
Одержали неявну функцію. Диференціюємо обидві частини рівності, з огляду на те, що ln у є складною функцією від х, та у залежить від х:
Звідси знаходимо:
Похідні вищих порядків
| Похідна функції y = f(x), в загальному випадку, також є функцією, тому її також можна диференціювати. В результаті одержимо функцію, що називається похідною другого порядку або другою похідною функції f(x). |
Її позначають одним із символів: у", 
.
Читається: у" - (ігрек два штрих), - (де два ігрек по де ікс квадрат).
Якщо S = f(t) - закон прямолінійного руху точки, то, за визначенням, прискорення руху в момент часу t дорівнює другій похідній 
. Це означення природно відображає суть прискорення як швидкість зміни швидкості.
| Диференціюючи похідну другого порядку, одержимо похідну третього порядку або третю похідну. |
Її позначають одним із символів: 
. Читається: 
- (ігрек три штрих), 
- (де три ігрек по де ікс куб).
| Похідна п-го порядку – це похідна від похідної (п - 1)-го порядку. |
Позначення:
.
Позначення за допомогою штрихів вживаються до похідної 3-го порядку. Далі застосовують позначення:
або 
.
Приклад 2.43. Зайти другу похідну від функції: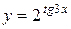 
.
Розв’язання. Перша похідна: 
Вона представляє собою добуток сталої величини 
та двох функцій від х 
Тому
Приклад 2.44. знайти другу похідну від функції:
.
Розв’язання.
Перша похідна: 
.
Приклад 2.45. знайти четверту похідну від функції:
.
Розв’язання. 
, 
, 
,
.
Приклад 2.46. знайти похідну четвертого порядку від функції: 
.
Розв’язання. 
Зауваження. Функція має похідну будь-якого порядку.
Диференціал
Диференціалом функції в точці х називається добуток похідної функції в цій точці на приріст аргументу:
 (2.17)
|
Диференціал функції - це умовний приріст, якого функція набула б на відрізку 
за умови, що вона змінюється в інтервалі рівномірно, зберігаючи ту швидкість, що мала на початку інтервалу. У цьому полягає суть диференціала.
Знайдемо диференціал функції 
. Маємо 
. Таким чином, диференціаларгументудорівнює приросту аргументу, тобто диференціал функції можна записати у вигляді dy = y'dx.
Диференціал функції у вигляді dy = y'dx застосовується набагато частіше. Це пов’язано з тим, що записаний у вигляді dy = y'dx диференціал має важливу властивість інваріантості, яка полягає у тому, що форма диференціалу dy = y'dx не залежить від того, чи є х незалежною змінною чи залежить від іншого аргументу.
Приклад 2.47. Знайти диференціал функції: 
Розв’язання. Знаходимо похідну функції
Розглянемо співвідношення між приростом функції і її диференціалом при 
. З визначення похідної 
випливає, що 
або 
(2.18)
при 
. 
- нескінченно мала вищого порядку малості у порівнянні не тільки з , але і з 
, тому диференціал є головною частиною приросту функції. На цьому засновано використання диференціалу для наближених обчислень:
. (2.19)
Приклад 2.48. обчислити наближено 
.
Розв’язання. Представимо 
Використаємо як математичну модель функцію 
. За формулою (2.17) отримуємо:
.
Приймаємо 
, та 
.
