Інтервали монотонності і екстремум функції
Достатня умова зростання та спадання функції на інтервалі.
якщо в усіх точках деякого інтервалу перша похідна 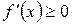 , то функція на цьому інтервалі не спадає. якщо у всіх точках деякого інтервалу перша похідна
, то функція на цьому інтервалі не спадає. якщо у всіх точках деякого інтервалу перша похідна 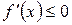 , то функція на цьому інтервалі не зростає.
, то функція на цьому інтервалі не зростає.
Неперервна на інтервалі зростаюча або спадна функція називається монотонною (рис. 2.7, 2.8).
Рис. 2.7 і 2.8 ілюструють той факт, якщо функція у = f(x) зростає (спадає), то похідна 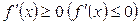 . Дійсно, на рис. 2.7 функція зростає і a -кут нахилу дотичної гострий, тобто f'(x) = tga > 0. А на рис. 2.8 функція спадає і a - кут нахилу дотичної a тупий, тобто
. Дійсно, на рис. 2.7 функція зростає і a -кут нахилу дотичної гострий, тобто f'(x) = tga > 0. А на рис. 2.8 функція спадає і a - кут нахилу дотичної a тупий, тобто 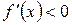 .
.
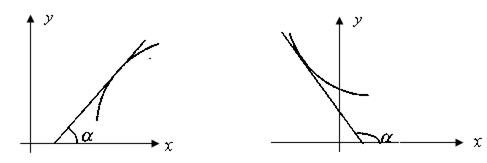
Рис. 2.7 Рис. 2.8
Таким чином, для того, щоб знайти інтервали зростання (спадання) функції, треба знайти похідну і розв’язати нерівність 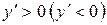 . При цьому необхідно враховувати область визначення функції.
. При цьому необхідно враховувати область визначення функції.
Приклад 2. 49. Знайти інтервали монотонності функції 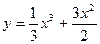 .
.
Розв’язання. Функція, що розглядається, многочлен. Тому область визначення функції 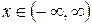 , в якій вона неперервна.Знаходимо похідну функції
, в якій вона неперервна.Знаходимо похідну функції
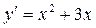 .
.
Прирівнюємо похідну до нуля для того, щоб визначити критичні точки, у яких похідна розглянутої функції дорівнює нулю.
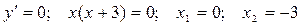
Критичні точки 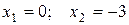 поділяють область визначення функції на інтервали, в яких похідна не змінює знак. Відомим зі школи методом інтервалів визначаємо знак похідної і тим самим визначаємо інтервали зростання та спадання функції (рис. 2.9).
поділяють область визначення функції на інтервали, в яких похідна не змінює знак. Відомим зі школи методом інтервалів визначаємо знак похідної і тим самим визначаємо інтервали зростання та спадання функції (рис. 2.9).
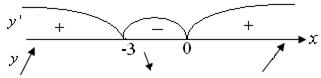
Рис. 2.9
При 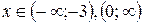 , у ' >0, і функція зростає. при
, у ' >0, і функція зростає. при 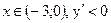 і функція спадає. Таким чином, розглянуті інтервали будуть інтервалами монотонності.
і функція спадає. Таким чином, розглянуті інтервали будуть інтервалами монотонності.
Екстремум функції.
| Точки з області визначення функції, у яких у' = 0, або у' = ¥, або у' не існує (як скінченна, так і нескінченна), називаються критичними точками І-го порядку. Критичні точки повинні належати області визначення функції. | |
Якщо для всіх значень точок х з деякого околу точки 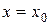 виконується нерівність виконується нерівність 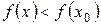 , то , то 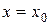 називають точкою локального максимуму.
Якщо для всіх значень точок х з деякого околу точки називають точкою локального максимуму.
Якщо для всіх значень точок х з деякого околу точки 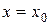 виконується нерівність виконується нерівність 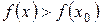 , то , то 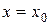 називають точкою локального мінімуму. називають точкою локального мінімуму.
| |
| Мінімум та максимум функції називають її екстремумами. | |
Розглянемо необхідну та достатні ознаки екстремуму функції.
Необхідна ознака екстремуму. В точках з області визначення функції, у яких
у' = 0, або у' не існує, може бути екстремум.
Не в кожній критичній точці обов'язково буде екстремум. Ці точки треба досліджувати за одним з наступних правил (достатні ознаки екстремуму).
Достатні ознаки екстремуму.
1. Якщо при переході через критичну точку х0 похідна змінює знак (зліва) з плюса на мінус (справа), то х0 - точка максимуму (відбувається перехід зі зростання на спадання). Якщо похідна змінює знак з мінуса на плюс, то х0 - точка мінімуму (відбувається перехід зі спадання на зростання). Якщо похідна знак не змінює, то в точці х0 екстремума немає.
2. Якщо в критичній точці х0 від’ємна друга похідна, тобто 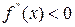 , то х0 - точка максимуму. Якщо ж
, то х0 - точка максимуму. Якщо ж 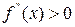 , то х0 - точка мінімуму. Якщо
, то х0 - точка мінімуму. Якщо 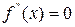 , то в точці х0 екстремума немає.
, то в точці х0 екстремума немає.
Приклад 2.50. Знайти точки екстремуму функції 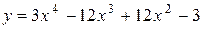 .
.
Розв’язання. Знаходимо першу похідну функції:
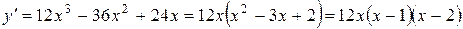 .
.
Критичні точки знайдемо з умови у' = 0: 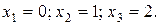
Визначимо знак похідної при переході через критичні точки (таблиця 1) за першою достатньою ознакою екстремуму.
Таблиця 1
| х | 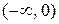
| 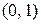
| 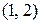
| 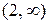
| |||
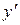
| - | + | - | + | |||
    у у
| min | max | min |
Отже, x1 = 0, х2 = 2 - точки мінімуму, х = 1 - точка максимуму. Визначимо їх величини:
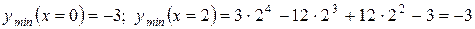 :
:
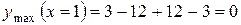 .
.
Зауважимо, що в таблиці містяться також інтервали монотонності функції, на які поділяється вся вісь ОХ критичними точками. У таблицю варто включати і точки розриву, але дана функція неперервна при будь якому х.
Приклад 2.51. Знайти екстремуми функції  за допомогою другої похідної.
за допомогою другої похідної.
Розв’язання. Перша похідна:
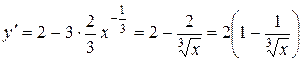 .
.
Знаходимо критичні точки, у яких перша похідна 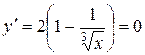 .
.
Це лише одна точка 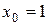 .У точці х =0 похідна не існує.
.У точці х =0 похідна не існує.
Друга похідна:
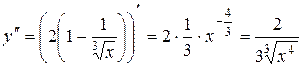 .
.
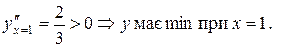
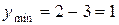 .
.






