Наиболее характерные и опасные интермодуляционные помехи образуются на следующих частотах:
сигнала — ыпх2 ± <о„х1 — шс, 2to nxi — wnx2 = шс, 2сопх2 — юпх1 =
= щ',
зеркального канала и прямого прохождения -- сопх1 + сопх2 — а>зк, сопх2 zb с0пх1 = wn.
Коэффициент нелинейных искажений составляющих интермодуляции второго порядка (шпх1 ± юПхг) двух немодулированных помеховых сигналов (7ПХ] cos conx] (и Unx2 cos сопх2/ |П]:

а третьего порядка (2co„Xi ± о>пх2) или двухсигнальный коэффициент нелинейных искажений
 где Кп - резонансный коэффициент усиления до входа каскада; (шпхьг) — нормированные значения АЧХ на соответствующих частотах помех до входа каскада; S, 5<п) — крутизна и ее производные по входному напряжению нелинейной вольт-амперной характеристики активного прибора каскада.
где Кп - резонансный коэффициент усиления до входа каскада; (шпхьг) — нормированные значения АЧХ на соответствующих частотах помех до входа каскада; S, 5<п) — крутизна и ее производные по входному напряжению нелинейной вольт-амперной характеристики активного прибора каскада.
Механизм перекрестных искажений в приемнике описан в § 1.3. Для приемников АМ-сигналов характерны существенные амплитудные перекрестные искажения. Аппроксимируем вольт-амперную характеристику электронного прибора (нелинейного элемента) рядом Тейлора, ограничившись двумя членами:;вЫХ — SuBX+ S"
+ зГ "3вх. гДе 5 и S" — крутизна и
ее вторая производная по входному напряжению.
Представим входное напряжение в виде суммы тональных АМ-сигнала и помехи:

(15.35)
где тс и тпх — коэффициенты амплитудной модуляции сигнала и помехи.
Подставив мвх в выражение для 1пых и считая, что последующие избирательные цепи отфильтровывают колебания всех частот, кроме частоты сигнала юс и близких к ней, получим

В результате детектирования напряжение низкой частоты будет содержать частоты модуляции сигнала Qv и помехи QIIX. Амплитуды этих составляющих
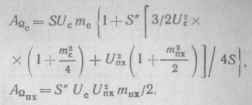
Отношение амплитуд указанных составляющих называется коэффициентом перекрестной модуляции (1 .7):

который пропорционален коэффициентам модуляции помехи и сигнала, параметру S"/S, квадратам амплитуд помехи и сигнала. Граничным значением коэффициента перекрестных искажений считается величина
(KneJrp < Ю %.
Перейдем к оценке явления блокирования (см. § 1.3) приемника АМ-сигналов. Пусть на входе произвольного каскада высокочастотной части приемника с нелинейной вольт-амперной характеристикой вида /вЫх =  дей-
дей-
ствует входная смесь в виде суммы тональных АМ-сигнала и помехи (15.35). При этом будем считать, что амплитуда сигнала значительно меньше амплитуды помехи (Uc С с/пх), а частота помехи сопх не совпадает с частотой сигнала о>с.
Составляющая тока активного прибора с частотой полезного сигнала, которая будет селектироваться избирательной цепью,
Относительное изменение амплитуды этого тока под воздействием помехи и является коэффициентом блокирования:

где /Шс = SUC — амплитуда тока сигнала в отсутствие помехи.
При немодулированной помехе полагают тпх = 0. Граничное значение коэффициента блокирования в обычных приемниках (кбл)гр < 0,2.
Нелинейность вольт-амперной характеристики активного прибора приводит также к явлению сжатия амплитуды полезного АМ-сигнала (см. § 1.3). Вновь представляя 'вых ("вх) в виде укороченного ряда Тейлора и считая ивХ = ■ — Uc (1 + mc cos Qct) cos юсг, найдем выражение для тока частоты сос, которая фильтруется в избирательных цепях приемника:



Граничным коэффициентом сжатия считают величину (ксж)гр < <0,1ч-0,2. Из выражения для i„ видно также, что нелинейность вольт-амперной характеристики приводит к искажениям огибающей АМ-сигнала, т. е. к появлению в спектре огибающей второй и более высоких гармоник модуляции, что выявляется после детектирования.
Коэффициент нелинейных искажений (по второй гармонике) огибающей АМ-сигнала равен отношению амплитуд токов второй гармоники модуляции к первой:

§ 15.4. Приемники ЧМ-и ФМ-сигналов
Поставим задачу определения структуры оптимального приемника ЧМ-сигнала, когда на его вход воздействует сумма полезного сигнала и шума (1 5.2). Задача приемника состоит в оптимальном выделении сообщения X (t) из входной смеси (t).
Рассмотрим реальный случай, когда в точке приема известны все параметры принятого сигнала, за исключением двух: информационного сообще-
ния X {t) и случайной фазы ц> (/). Тогда сигнал описывается формулой
uc(t, Х,) = A>cos(<»cH ■Ф(г)), (15.39)
Где

Характер изменения случайной фазыг|з (/) и сообщения X (/) описывается априорными дифференциальными уравнениями вида

(15.40)
где ыф (0 ь= с1ф/с1/ и «я, (г) — взаим-нонезависимые белые фазовые и информационные шумы с известными статистическими характеристиками.
По условию амплитуда Л0, частота со„ и крутизна характеристики частотного модулятора Мц — постоянные и. известные величины. Статистические характеристики входного шума ищ (t) также известны.
Структуру оптимального приемника находят с помощью алгоритма (15.8). Для ЧМ-сигнала (15.39) из (15.8) получаем два дифференциальных уравнения фильтрации:
для оценки фазы г|> из (15.40) при
коэффициенте сноса а (т|э) МЧХ,

(15.41)
для оценки сообщения из (15.40) при коэффициенте сноса а (X,)
= — ocXf

(15.42)
где crj, — дисперсия апостериорного распределения фазы: а - коэффициент взаимной корреляции сообщения и фазы. ■
Сообщение в (15.39) закодировано в законе изменения фазы сигнала,
поэтому для определения функции / (/, г|)) используется формула (15.5):

(15.43)
а производная по фазе

Подставляя производную в дифференциальные уравнения фильтрации (15.41), (15.42) и решив их, получим алгоритмы, моделирующие структуру оптимального приемника ЧМ-сигналов:

(15.44)

(15.45)
где Kt = 2ka^A0/N0\ К2 = 2а* AJ /5УЭ Л/о — коэффициенты передачи усилителей; Т — \1а - постоянная времени /?С-цепи.
Структурная схема оптимального приемника ЧМ-сигналов, моделирующего уравнения (15.44), (15.45), приведена на рис. 15.8. После линейной части приемника смесь полезного сигнала и шума»£ (/) подается на перемножитель (фазовый детектор).
куда одновременно поступает опорный сигнал с частотой, равной частоте полезного сигнала и оценочным
значениям фазы \р. Верхний канал — информационный, моделирующий уравнение (15.44), состоит из перемножителя, усилителя с коэффициентом усиления Ki и интегрирующей RC -ne-
пи. Оценочное значение фазы ф, согласно (15.45), вырабатывается каналом типа ФАПЧ, осуществляющим слежение за полной фазой принимаемого сигнала. Отличительной особенностью системы ФАПЧ является то. что регулировка фазы перестраиваемого генератора (ПГ) с помощью управляемого элемента (УЭ) осуществляется по двум каналам: с выхода информационного канала с коэффициентом передачи Мц/S уэ и с выхода перемножителя с коэффициентом передачи Кг- Приемник типа следящего устройства осуществляет квазикогерентный прием ЧМ-сигнала, так как фаза сигнала не равна ее оценке (г|>, Ф
Ф ф), выработанной системой ФАПЧ.
Далее рассмотрим структуру оптимального приемника ФМ-сигнала. Постановка задачи аналогична рассмотренной для ЧМ-сигнала, поэтому повторять ее не будем.
Полезный ФМ-сигнал описывается формулой

где 9 (г) = МФ X (г) + ср (/), МФ — крутизна характеристики фазового модулятора.
Кроме сообщения X (г) и случайной фазы ср (/), все остальные пара-
метры сигнала считаются известными в точке приема.
Априорные дифференциальные уравнения, описывающие изменения
фазы 9 (/) и сообщения X (/). имеют вид
 (15.47)
(15.47)
Структуру оптимального приемника находят на основе алгоритма оптимальной стационарной фильтрации (15.8). Для ФМ-сигнала (15.46) из (15.8) получаем два дифференциальных уравнения фильтрации:
для оценки фазы из (15.47)
при коэффициенте сноса а (9) — = — аМф Xt
 (15.48)
(15.48)
для оценки сообщения из (15.47) при коэффициенте сноса а (X) — — аХ
 (15.49)
(15.49)
где Og- — дисперсия апостериорного распределения фазы; § — коэффициент взаимной корреляции сообщения и фазы.
Функция / (t, 9) и ее производная
67 (t, 9)/6? такие же, как в (15.43). Подставляя производную в (15.48), (15.49) и решив эти дифференциальные уравнения, получим алгоритмы, моделирующие оптимальную структуру приемника ФМ-сигналов:


(15.51)
где К[ = 2k£ hAn/N„; К'2 = 2a\AJ /SyaA/,, коэффициенты передачи усилителей; Т — 1/а — постоянная времени /?С-цепи.
Структурная схема оптимального приемника ФМ-сигналов, моделирующего уравнения (15.50), (15.51), приведена на рис. 15.9. Как и в случае ЧМ-сигнала (см. рис. 15.8), оптимальный демодулятор ФМ-сигнала осуществляет квазикогерентную обработку сигнала и состоит из информационного канала и сложного ФАПЧ для создания опорного сигнала на перемножитель. Структурно схемы оптимальных приемников ФМ- и ЧМ-сигналов подобны и отличаются только знаками алгебраического суммирования управляющих напряжений, подаваемых на управляющий элемент (УЭ), а также коэффициентами передачи всех трех усилителей. Отметим, что в коэффициенты передачи входят как известные по условию параметры (Ло, N0, 5уэ), так и вычисляемые по формулам [29, 301 дисперсии сг~,
и коэффициенты взаимной корреляции к£ ь.
Перейдем к рассмотрению н е -когерентного приемника ЧМ (ФМ)-сигнала, когда для демодуляции не используется опорный сигнал с информацией о фазе полезного сигнала. Структурная схема подобного приемника ЧМ-сигнала приведена на рис. 15.10. Принимаемая смесь сигнала и шума преобразуется в смесь на промежуточной частоте, усиливаемую УПЧ, полосу пропускания которого выбирают из условия практически неискаженного прохождения ЧМ-сигнала и ослабления шумов за пределами полосы. Поскольку полезная информация заложена в законе изменения частоты сигнала, с помощью амплитудного ограничителя (АО) ослабляется паразитная амплитудная модуляция сигнала. В качестве демодулятора используется частотный детектор (ЧД), выходное напряжение которого пропорционально разности между мгновенной и промежуточной частотами. Усилитель нижних частот (УНЧ) удаляет, насколько это возможно, шумы и комбинационные частоты выше частот полезной информации. Структура стандартного прием-

Рис. 15.9
ника ЧМ-сигнала изображена с системой АПЧ гетеродина Г, состоящей из ЧД, фильтра Фапч, пропускающего только медленные изменения частоты, обусловленные нестабильностью гетеродина и передатчика, а также управляющего элемента (УЭ). Благодаря наличию АО в приемниках ЧМ-сигнала часто не применяется система АРУ. Последняя используется только в приемниках с большим диапазоном уровней входного сигнала. В многоканальных радиолиниях с ЧМ в приемнике для разделения каналов после ЧД используется набор полосовых фильтров, настроенных на частоты модуляции каналов.
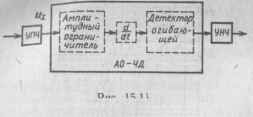
Для сравнения помехоустойчивости оптимальных (квазикогерентных) и неоптимальных (некогерентных) приемников ЧМ-сигналов необходимо провести анализ помехоустойчивости стандартных частотных демодуляторов. К ним относятся ЧД на связанных и расстроенных контурах, частотно-импульсные ЧД и др. (см. § 7.5). Функционально амплитудный ограничитель — частотный детектор (АО — ЧД) — можно представить структурной схемой, содержащей ограничитель, дифференцирующее звено и детектор огибающей (рис. 15.11), а также додетекторный (УПЧ) и по-следетекторный (УНЧ) фильтры-усилители. Колебание на входе АО

Рис. 15.10 287
Рнс. 15.11
представляет собой аддитивную смесь полезного сигнала ис (/, X) и нормального шума иш (/) со средней частотой шш = со(. и спектром, ограниченным шириной полосы пропускания УПЧ:

где R (/) — огибающая суммарного
t
колебания; ф (/) Мч \ X (т) dx —
о
полезная фаза сигнала

— шумовая фаза; х (t) = Um(t )x
XCOS фш (t),y(t) = иш (t) вШфш (О —
квадратурные огибающие шума.
Сигнал и шум в векторном представлении показаны на рис. 15.12. Векторное сложение сигнала и шума дает результирующий вектор огибающей R (/) и шумовую фазу 9Ш (/). Далее предполагается, что амплитудный ограничитель полностью убирает амплитудную модуляцию с R (t) и оставшийся процесс с постоянной амплитудой проходит через дифференцирующее звено (см. рис. 15.11), на выходе которого имеем


т. е. дифференцирующее звено преобразует ЧМ-колебание в амплитудно-частотно-модулированное с законом изменения амплитуды Л' Icoc -f-ip (/)-f-+ 9Ш (t)]. Включенный далее детектор огибающей выделяет именно ее, а в случае балансного детектора при этом устраняется постоянная составляющая А 'шс. Следовательно, на выходе детектора огибающей
"д =КдЖ0 +е ш(0]. (15.54)
где, согласно (15.52), производная полезной фазы ф (г) = Мч X (t) — мгновенная девиация частоты, обусловленная сообщением X (г).
Шум на выходе ЧД0Ш<7) имеет нормальное распределение, так как дифференцирование является линейной операцией над нормальным шумом 9Ш (t).
Перейдем к оценке помехоустойчивости. Чтобы установить связь между отношениями сигнал/шум на выходе и входе демодулятора, необходимо знать амплитудно-частотные характеристики (АЧХ) УПЧ и УНЧ, а также энергетические спектры сигнала и шума. Предположим, что эти АЧХ идеальные, т. е. имеют прямоугольную форму. Сообщение X (t) представляет собой нормальный случайный процесс и его.спектральная плотность лежит в полосе от нижней /н до верхней /в частоты. Из (15 .53) следует, что коэффициент амплитудной модуляции по сообщению /пА => = |tp|c к /tOc- Тогда мощность выходного сигнала
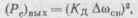
(15.55)
где Ао)ск — среднеквадратическое значение девиации частоты.
Вначале рассмотрим случай большого отношения сигнал/шум на входе частотного демодулятора (Ап У?> х (/), у (/)). При таком условии шумовая фаза вш (/) мало зависит от модуляции сигнала. Поэтому в (15.52) выражение для фазы упростится:
нш (0 «У <0''Л„. Согласно (15.54), шум на выходе детектора огибающей
Ш(0 y(t)iAlt.
Найдем теперь спектральную плотность Gy (to) шума. Так как происходит процесс дифференцирования, то

(15.56)
где Gy (to) iV0 — спектральная плотность процесса у (/).
Полная мощность шума на выходе ФНЧ в полосе сообщения (до верхней частоты /в)

Отношение сигнал/шум на выходе можно найти из выражений (15.55) при /Сд = 1 и (15.57):

(15.58)
где тск - A/ck/Fj, — среднеквадра-тическое значение индекса ЧМ,
 - отношение
- отношение
сигнал/шум на входе в полосе сообщения 2/в.
Из (15.58) находят обобщенный выигрыш в помехоустойчивости при частотной модуляции:

(15.59)
Отметим, что если бы сообщение Я (г) представляло собой не случайный процесс, а однотональную модуляцию частоты FM, то изменилась бы только мощность сигнала на выходе ЧД: вместо (15.55) получилось бы равенство {'Р~с)вых == Дсо2,пах/2 и обобщенный выигрыш

(15.60)
где т Afmax/FM — индекс ЧМ.
В формулах (15.59), (15.60) входной шум измеряется в удвоенных полосах сообщения 2FB (2FM). Если же мощность шума оценивать во всей требу-
емой полосе частот, занимаемой ЧМ-сигналом А/с ^-2(1 + т) F„, то выигрыш в помехоустойчивости

(15.61)
Приведем физическое объяснение выигрыша в помехоустойчивости. Демодулятор ЧМ-сигнала преобразует равномерный энергетический спектр шума G (/) = N 0/2 при / — 1/2А/с < / < / + 1/2Д/с на входе ограничителя (в УПЧ) в спектр с параболической огибающей 1см. (15.56)1 на выходе ЧД. Стоящий на выходе УНЧ пропускает этот шум только до частот сообщения FB (FM), т. е. из области вблизи начала параболы, где спектральная плотность шума мала (рис. 15.13). Этим и объясняется увеличение отношения сигнал/шум на выходе демодулятора ЧМ-сигнала.
Кратко рассмотрим помехоустойчивость приемника ФМ-сигнала. Исходная запись смеси ФМ-сигнала и шума подобна (15.52), только полезная фаза сигнала

(15.62)
Если такую смесь подать на обычный ЧД, реагирующий на изменение мгновенной частоты, то выходное напряжение будет пропорционально производной фазы входной смеси (15.54). При детектировании колебаний с медленно изменяющейся полезной фазой (при речевом или тональном сообщении) стандартный ЧД (см. рис. 15.11) после детектора огибающей
дополняется корректирующей интегрирующей цепью с частотной характеристикой АГи-зв (/со) = 1 //ю- После нее полезный сигнал пропорционален (15.62), а шум — фазе 9Ш (/).
Мощность полезного сигнала в этом случае пропорциональна отклонению фазы, т. е. индексу модуляции
 (15.63)
(15.63)
Для определения выходного шума надо записать спектральную плотность на выходе интегрирующего звена через спектральную плотность на его входе и коэффициент передачи интегрирующего звена /Си.зв. (/со). Используя (15.56), имеем

Отношение сигнал/шум на выходе находят с помощью выражений (15.63) и (15.64) ■
I 
где <7ВХ = (А Ц2) I (N0FM) — отношение сигнал/шум на входе в полосе сообщения 2 FM.
Обобщенный выигрыш в помехоустойчивости при фазовой модуляции
5фм = с/вых/?вх = '"2- (15.65)
Сравнивая обобщенные выигрыши в помехоустойчивости при однотональной модуляции для ЧМ (15.60) и ФМ (15.65), видим, что помехоустойчивость при ЧМ выше, чем при ФМ. При ЧМ и ФМ обобщенные выигрыши пропорциональны квадрату индекса угловой модуляции, что объясняется тем, что шум в этих системах проявляется в виде фазового шума.
Указанные свойства частотных (фазовых) демодуляторов справедливы только при большом отношении сигнал/шум на их входе, что позволяло записать шумовую фазу в виде 6Ш(/) «у (t)/A0. При уменьшении отношения сигнал/шум в ЧМ (ФМ)-демодуляторах наступает явление порога, при котором линейная зависимость выигрышей В' уже не подчиняется формулам (15.59), (15.60),(15.65), а выявляются нелинейные зависимости между отношением сигнал/шум на выходе демодуляторов (<7ВЫХ) от подобного же отношения на входе (qBX). На рис. 15.14 показаны типичные надпороговая и подпороговая области. Важной закономерностью этих графиков является то, что для стандартных демодуляторов пороговое значение qBX возрастает по мере увеличения индекса модуляции т. На этом же рисунке приведена зависимость <7вЫХ (qBX) (пунктирная линия) для оптимального демодулятора, который рассматривался в начале данного параграфа. При больших отношениях qBX она совпадает с этими значениями для стандартного демодулятора, а при уменьшении qBX порог в оптимальном демодуляторе проявляется при более низких значениях <7ВХ. Таким образом, использование оптимального демодулятора позволяет вести прием ЧМ (ФМ)-сигнала в пороговой и подпороговой областях работы стандартного демодулятора.
Перейдем к физическому объяснению явления порога в ЧМ (ФМ)-де-модуляторах. Для облегчения пони-
мания предположим, что несущая частота немодулирована. Сигнал и шум представим в виде векторов (рис. 15.15, а, в), причем отобразим лишь относительное вращение результирующего вектора по отношению к сигнальному. Когда вектор шума мал (рис. 15.15, а), он вызывает незначительные флуктуации мгновенной частоты относительно промежуточной со„ (рис. 15.15, б). Если же вектор шума большого уровня (рис. 15.15, в), то результирующий вектор принимаемой смеси сигнала и шума описывает своим концом замкнутую траекторию вокруг начала координат. Это вызывает фазовую ошибку, равную 2л. При быстром скачке фазы появляется кратковременный импульс мгновенной частоты (рис. 15.15, г) с практически равномерным спектром на выходе демодулятора. Следовательно, характер спектральной плотности шума Сц (ш) в области частот сообщения на выходе демодулятора меняется. Если при большом отношении сигнал/шум на входе демодулятора имелось параболическое спектральное распределение на выходе (см. рис. 15.13), то при уменьшении этого отношения за счет импульсного шума происходит перераспределение энергии: спектраль-
ная плотность в низкочастотной области возрастает. Именно этим и объясняются пороговые явления в демодуляторах сигналов с угловой модуляцией.
§ 15.5. Прохождение ЧМ (ФМ)-сигнал а через линейную часть приемника
При прохождении ЧМ (ФМ-сигнала через линейную часть приемника (до демодулятора) возникают линейные и нелинейные искажения передаваемых сообщений. Основная причина искажений — неравномерность амплитудно-частотной и кривизна фазо-частотной характеристик линейного тракта. Выбор рационального метода исследования искажений зависит от соотношения между параметрами линейного тракта и параметрами модуляции сигнала. Если число составляющих спектра ЧМ (ФМ)-сигнала, попадающих в полосу пропускания 2Дсоф тракта, равно 2Дс0ф/й < Зн-5, то наиболее рациональным является спектральный метод исследования, заключающийся в суммировании мгновенных значений составляющих спектра. В этом случае метод анализа прохождения ЧМ-коле-баний через линейный тракт приемника подобен изложенному в § 15.3 для АМ-колебаний. При соотношении 2Дсоф/£2 > 1 использование спектрального метода сопряжено с большими вычислительными трудностями и применяется метод мгновенной частоты (без разложения в спектр). Основное значение при этом приобретает относительная скорость изменения частоты сигнала, характеризующая длительность t0 нахождения мгновенной частоты в полосе 2Дыф. Мерой инерционности линейного тракта с полосой 2Дсоф по отношению к ЧМ, характеризуемой девиацией Дсод и частотой модуляции Q, является соотношение
где х = 1/Дшф постоянная времени линейной цепи.






