Разновидности метода статис ческих эквивалентов. Метод экви лентов (при детерминированных в* действиях) или статистических, вивалентов (при случайных воздей виях) состоит в замене реального з: на радиосистемы или радиоустроЙ! ва математической моделью, явля щейся эквивалентом этого звена. П этом статистический эквивалент зве обеспечивает адекватность выходнс сигнала лишь в статистическом смь ле, с точностью до заданных статист ческих характеристик.
Существует ряд методов замер реального звена эквивалентом и ст тистическим эквивалентом: формул ный, статистической линеаризаци гармонической статистической лине
нзации, генерации, фильтрации ин-ормационного параметра и др.
формульный метод редусматривает моделирование вы-одного случайного сигнала т] (г) иро-звольного звена в соответствии с налитической формулой связи с вход-ым случайным воздействием | (/) 1 общем случае векторным):
(0 = АШ'>}- (17.54)
При этом методе выходное воздей-гвие будет иметь необходимые ста- 4стические свойства всякий раз, ког-а правильно (как в реальной задаче) удут заданы статистические характе-истики входного воздействия £ (г), формула (17.54) выбрана достаточ-о достоверной.
Метод статистичес-о й линеаризации [51 рименяется для моделирования низ-очастотных нелинейных звеньев пу-;м их замены линейным статистиче-<им эквивалентом (по математическо-у ожиданию тц и флуктуации г|° = = г| — тп). В этом случае модель равильно воспроизводит лишь магматическое ожидание и простейшие гатистические характеристики (дис-ерсию, корреляционную функцию) ыходных флуктуации т)° (г).
Метод гармонической татистической линеа-и з а ц и и [5] является распро-гранением предыдущего метода на елинейные радиозвенья.
Метод генерации сво-ится к замене реального звена с вы-одным воздействием
генератором адекватного в статистическом смысле случайного процесса с точностью до заданных статистических характеристик. Для этого заранее аналитически находят статистику I (t) и сам сигнал s (г) и в модели с помощью ЭВМ производят их «генерацию» по исходным статистическим характеристикам входных воздействий | (t). Метод генерации наиболее удобен для моделирования крупных радиозвеньев или радиоустройств чаще разомкнутого типа.
Метод фильтрации информационного параметра заключается в замене реального нелинейного звена с выходным сигналом
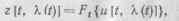(17.56)
зависящим от информационного параметра A (t), эквивалентным звеном, формирующим статистически эквивалентный сигнал
(17.57)
из самого информационного параметра А (/) с добавлением некоторого эквивалентного шума Енк (/). При этом функционалы F (/) и G (t) обычно существенно отличаются друг от друга. Данный метод применяют, как правило, для формирования математических моделей звеньев (в частности, дискриминаторов) следящих радиоустройств.
Примеры моделирования РПУ фор-, мульным методом. Рассмотрим один из примеров.
Пример 17 .5. Математическая модель типового РПУ. Рассмотрим вновь структурную схему РПУ
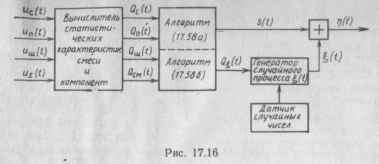
рис. 17.8 и возьмем за основу ее математическую модель рис. 17.14 (метод комплексной огибающей). Упростим эту модель путем объединения однотипных элементов и получим исходную модель рис. 17.15. Найдем систему алгоритмов описания функционала (17.54):
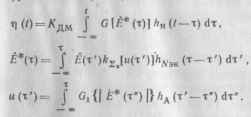
Эту систему уравнений можно представить совокупностью «математических блоков», выбранных относительно произвольно и не связанных со звеньями на рис. 17.15 [5]. Часто подобные модели используют для расчетов (методом Монте-Карло) отдельных реализаций выходных сигналов т] (t). Тогда к модели, полученной формульным методом, добавляют блок расчета статистических характеристик на выходе РПУ, в частности: математического ожидания < r| (t) >£_^0,— = <Т] U)>E = 0, сигнала s (/) = = т„ (/) — тЦг (а), помехи £(0 =1 W —
— s (/), дисперсии помехи of = <(ii —
— тч)2>, отношения сигнал/помеха q (t) =
= s2 (/)/2of «).
Примеры моделирования методом генерации. Пусть, например, поставлена задача смоделировать выходное напряжение ц (t) = s (t) + £ (0 типового РПУ рис. 17.8 при входной смеси
х (0 - "2 U) = ив (0 + «„ (0 + иш W-
Тогда для создания модели статистического эквивалента методом генерации вначале надо найти алгоритмы:
S(0 = s|f, Q c(0- Q n(0. QnAt), QCM(0],
(17.58a)
Qt(t) = <hit, Qc(t), Q„(t), Qm(t),
QcmWI. (17.586)
где Qc, Qu, Qm, QCM — статистические параметры сигнала, помехи, шума, смеси соответственно, a Qj — статистические параметры выходных флуктуации.
На основе полученных формул можно построить статистический эквивалент (рис. 17.16), в котором на выходе генерируются составляющие смеси под заданную статистику Qi (t). рассчитываемую в модели по формулам (17.58). Статистические характеристики Qc, Qu, Qm, QCM случайных процессов ис, ил, иш, и2 в модели можно найти как аналитически, так и методом Монте-Карло.
Пример 17.6. Математическая модель РПУ с амплитудной модуляцией. Найдем методом генерации статистический эквивалент типового звена РПУ, состоящего из трех последовательных звеньев: линейного радиоусилителя (ЛРУ) с резонансным усилением Км = Кв (/ш0) и эффективной полосой Д/в; квадратичного детектора с коэффициентом передачи Ккв, линейного низкочастотного усилителя (ЛНЧ) с усилением /Сно на постоянном токе и эффективной полосой AFH» Д/в'2-
Входную смесь постулируем в виде суммы Uj.. = «ci + "mi АМ-сигнала uci = Eei (t) cos (со„/ — ф0) и белого гауссова шума со спектральной плотностью G0-Найдем зависимости (17.58) методами статистической радиотехники.
На входе детектора будет присутствовать смесь АМ-сигнала нс (/) = £с (/) cos (со0/ — ф„); £с = К во Е с
(искажения сигнала в ЛРУ не учитываем)
и узкополосного гауссова шума «ш С) — = /? (О cos \щ( — 6 = А (/) cos со„/ + + В (I) sin щ1. Статистические характеристики этого шума равны: о2 = G0Kl0&fn,
га <т> = гв (Т) = °2гЛ' <Т>' ГЛВ (Т) =
—— гвд (т) - 0 (резонансная кривая ЛРУ симметрична), где г (•) — корреляционные и взаимнокорреляционные функции.
Считая квадратичный детектор идеальным, запишем напряжение смеси на его выходе: т)о (0 = ^кв£2 (0 = Ккп х X {£§ (0 + А* (0 + В2 (О -ь 2£с (О X X \А (/) cosifo + В (г) sin^0]}.
При выбранном широкополосном ЛНУ смесь ц = s ь £ на выходе типового звена будет состоять из сигнала s (/) = /Скв X X KmEl (t) и видеошума £ (0 = Л (/) —
- 1яч (/) = 2/С„в /С„о £с (/) М (0 cos ф0 + + В (/) sintyg]. Статистические характеристики этого шума равны: = 0, о2 (/) — = (2/Скв/С„0о)2 £сг (/), «5 (/, т) = <Е (О X X | (/ + т)> = (2К тКт а)2 £| (0 Гд, (т).
Приняв <?с (/) = £с (*), Qn. = lo2,
rjv(T)]. On ™ 9см = °. придем к СЭ рис. 17.16.
Примеры моделирования узлов РПУ методом фильтрации информационного параметра. Этот метод чаще всего применяют для нахождения СЭ дискриминаторов (Д) в типовых следящих радиотехнических устройствах (рис. 17.17).
