— F (/) X (/), где
матрица коэффициентов. 
При моделировании в схеме рис. 17.5 процессов кс, кп, А, В могут встретиться два случая.
В первом случае, когда процессы ке (t), а иногда и кП (/) детерминированы, применяют классические спектральные и временные методы из теории сигналов 111].
Во втором случае, когда параметры А,. (/), к„ (t) и шумовые процессы A {t), В (t) случайные, применяют методы статистической радиотехники, в частности метод «формирующего фильтра» 17]. Суть этого важного метода в скалярном варианте сводится к следующему.
Полагаем, что моделируемый случайный процесс к (t) сформирован путем пропускания белого гауссового шума nx (t) со спектральной плотностью Nx через стационарный линейный формирующий фильтр (ФФ) с передаточной функцией дробнорацио-нального типа (17.10). Это соответствует математической модели в виде стохастического дифференциального уравнения
A(p)k(t) = k,tB(p)nx(t), (17.28)
где А (р), В (р) — полиномы с неизвестными коэффициентами ah, Ьг, a k„ — некоторый коэффициент пропорциональности.
На выходе ФФ спектральная плотность процесса л (/)
(17.29)
Обычно при моделировании случайного процесса к (/) задают его корреляционную функцию Rx (т) или спектральную плотность Sx (а>). Тогда по формуле (17.29) методами фак-ториоции 171 восстанавливают сначала требуемую КЧХ ФФ К (/<й), а затем и ПФ К (р) В (р) I А (р). Далее путем сравнения с (17.10) находят неизвестные коэффициенты ah, b,. определяющие стохастическое дифференциальное уравнение (17.28).
Г (t) = 10... k0\T — матрицы коэффициентов размерностей тхп, nxl соответственно.
Искомый процесс A (t) связан с процессом X (0 матричным уравнением
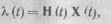(17.31)
где Н (t) = [10... 0] — матрица-строка размерности 1-я.
Матричная математическая модель формирования случайного процесса X (t) с помощью уравнений (17.30), (17.31) показана на рис. 17.6. Пунктиром обведен формирующий фильтр (ФФ), описываемый уравнением (17.30).
При моделировании статистически независимых шумовых процессов А (/), В (/) задают корреляционные функции <.ААТ> <ЙВТ> = г (т) [5] и используют метод формирующего фильтра от двух независимых датчиков нормальных случайных чисел.
Математические модели функциональных звеньев РПУ (библиотека моделей). С помощью общих соотношений (17.1) — (17.6) можно составить библиотеку математических моделей (в рамках метода несущей) основных типов функциональных звеньев РПУ, которые приведены в [51.
Часто прибегают к матричным методам моделирования, используя теорию многомерных марковских процессов. Так, задание уравнения (17.28) позволяет считать, что процесс X (О является составляющей «-мерного марковского процесса X (0 - [X, (t), Хп (t)V, где
МО.....*„(*) - dXn -tiWt.
Тогда стохастическому уравнению (17.28) для процесса X (0 будет соответствовать матричное дифференциальное уравнение для процесса X (t):
Так, линейные радиоусилител (ЛПУ) высокой или промежуточно частоты (ЛПУ), обычно регулируе мые схемой АРУ, следует моделирс вать в виде безынерционного усилите ля с коэффициентом усиления Кво) Х(«а) — для ЛРУ ИЛИ Кпо (яд) -для ЛПУ и стационарного ЛЗ с нор мированной импульсной характерг стикой /WO —Для ЛРУ или hnN(t)- для ЛПУ. При этом регулировочны кривые Кво («а) задаются при модел»
по
ровании в виде исходных данных.
В рамках метода несущей демод} ляторы (детекторы) принято мoдeл^ ровать в виде структурных схем, к(торые имеют место в реальных си< темах. Например, амплитудный д< тектор моделируют в виде последовг тельной схемы БНЗ с заданной нел1 нейной характеристикой у = G (х) низкочастотного линейного звена импульсной характеристикой Яд (г Для амплитудно-фазового (векторе мерного) и частотного детекторов и< пользуют классические схемы, npi веденные в настоящем пособии.
В процессе преобразований узк< полосных сигналов в различных р: диозвеньях выделить на их выходе о' дельно огибающую фазу и мгнове! ную частоту при моделировании ст; новится невозможным. Тем не мен«это бывает необходимо при иерехо; к таким схемам, как детекторы. Здес приходится применять сиециальнь методы формирования в ЭВМ огиб; ющих и фаз по узкополосным колеб; ниям, в частности, метод преобраз» вания Гильберта. Так, например, е< ли при моделировании сформирова узконолосный процесс и (0 = Е (t) XcosW гр(01. то в ЭВМ с п<
мощью преобразования Гильберта (ПГ) можно рассчитать ортогональный процесс v (t) х Е Ц) sin (— — тр (/)| +—+ и (t).
Пг
Тогда с помощью процессов и, v нетрудно сформировать огибающую Е (0, фазу ф (0 и мгновенную частоту сом (0: Е Ц) = [и* (0 + v2 (011/2. Ф (/) = о>0 t — arctg w(0/и (0. «м (0 = Ф' (0 - Е-1 iuv' — vu).
Если в модели рассчитаны огибающая и фаза, то в качестве моделей демодуляторов могут быть выбраны -идеализированные модели по методу комплексной огибающей (смешанное моделирование).
Примеры моделирования на основе принципиальных схем. Обычно входной сигнал (смесь) и схему моделируемого узла РПУ описывают дифференциальными уравнениями, а затем оцифровывают по правилам, изложенным в § 17. 3.
Пример 17.1. Модель амплитудного диодного детекто-р а (метод несущей). Рассмотрим схему классического амплитудного диодного детектора (рис. 17.7, а) с заданной вольт-амперной характеристикой t — О (ия). Она описывается нелинейным дифференциальным уравнением первого порядка
ay it)/dt + (\/rC)y(t)~(\/C)G[u(t) -
-У(*)] = 0. (17.32)
Объединив это уравнение с дифференциальным уравнением (17.27), получим структурную схему искомой модели детектора (рис. 17.7, б).
Можно применить другой метод моделирования, представив уравнение (17.32) в виде математической модели типового следящего РТУ (рис. 17.7, в). Здесь К (р) = = г/(1 + ргС) — передаточная функция гС-цепи в нагрузке детектора. Соответствующая цифровая модель детектора, показанная на рис. 17.7, г, является частным случаем модели рис. 17.4, б.
Примеры моделирования на основе структурных схем. С помощью указанной библиотеки программ [5] можно «набрать» поблочно математическую модель любого радиотехнического устройства, в частности, РПУ.
Пример 17.2. Модель супергетеродинного РПУ с амплитудной модуляцией. Пусть требуется методом несущей построить модель типового супергетеродинного приемника для приема АМ-сигнала в сопровождении имитационной помехи и неинформативного шума. С целью уменьшения объема моделирования полную структурную схему приемника несколько сокращают, соединяя в единые звенья однородные элементы (входную цепь и все каскады радиоусилителей — в единое звено ЛРУ, все каскады УПЧ — в единое звено ЛПУ и т. д.). Поэтому моделирование можно начать с сокращенной структурной схемы приемника (рис. 17.8).
На рис. 17.9 приведена полная структурная схема математической модели, полученной указанным методом |5]. Подроб ную модель можно описать полной системой интегродифференциальных уравнений,
связывающих выходное у (t) -- х\ (/) и входное х (t) — их (/) напряжения модели радиоприемника.
§ 17.5. Математическое моделирование РПУ методом комплексной огибающей
Математическая модель смеси на входе РПУ. В рамках метода комплексной огибающей вместо соотношений (17.22), (17.23) используют запись и2 = Re (Ёе'^') = = Re(£t.e/0V) + Re(£„e /u)n') 4-; ^е (/?e/w«'). Отсюда следуют алгоритмы формирования комплексной огибающей смеси:
Математическая модель комплексной огибающей смеси, построенная по алгоритмам (17.33) — (17.35), приведена на рис. 17.10. Здесь, так же как и в схеме рис. 17.5, главным является моделирование низкочастотных процессов Ас, Лп, А, В.
Математические модели функциональных звеньев РПУ (библиотека моделей). Суть метода комплексной огибающей (51 сводится к замене реальных радиозвеньев с узкополосными колебаниями на входе эквивалентными звеньями (ЭЗ) низкочастотного типа, связывающими комплексные огибающие на входе и выходе. Нахождение математического описания ЭЗ составляет основную задачу метода комплексной огибающей. В [5] приведены правила перехода от реальных звеньев к эквивалентным и составлена библиотека моделей. Напом-
ним основные положения метода комплексной огибающей.
Математические модели линейных радиозвеньев. Для стационарных линейных радиозвеньев (ЛРЗ) (рис. 17.11, а) с заданной импульсной характеристикой h (t) = Re {Н (t) X xe/[<at<-«И*)]} эквивалентное звено (математическая модель) имеет импульсную характеристику (рис. 17.11. б) вида
(17^
где сос — частота входного сигнала, а Дсос == со,. — <о0 — частотная расстройка.
Стационарные ЛРЗ можно моделировать спектральным методом. Для этого ЛРЗ с заданной КЧХ К (/со) — = у (co)/jc (со) (рис. 17.12, а) должно иметь в качестве модели КЧХ эквивалентного звена:
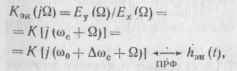
(17.37)
где ПРФ — индекс преобразования Фурье.
Комплексные частотные характе -ристики вида (17.37) называются укороченными и для их нахождения разработан ряд методов [51.
Так, для одиночного резонансного контура (усилителя) известна нормированная КЧХ [11]: KN(M = КШ/К+ Q
где а — 2 — (со — со0) — обобщенная рас-стройка; Q — io,Lr — добротность; со0 = = \/~[/LC — резонансная частота. Тогда по формуле (17.37) находим
*эк* </") >«*»Ц «»о + Асос + 0)1 щ
= Во 0'AcoR) [ 1 + At (/Дсос) /О]-', (17.38)
где В„ ОДсос) = ((o0/2Q); Ах (/Дшс) = [1 -|-+ 2 (Q/ci>„) /Дшс] — комплексные коэффициенты.
Для полосового резонансного усилителя с одинаково настроенными контурами КЧХ
* /■, — У(М'-Р*>
имеет вид KN (yw) = (] + /Чх)а _<_ р2 • где
Р — фактор связи. Тогда формула (17.37) дает следующую укороченную КЧХ:
K3KN (jQ) = В0 О'Дсос) [ 1 + (/Дсос) /О +
+ Л2(/Дшс) (/О)»]-». (17.39)
Здесь В0 (/Дсос), Л;(/Дсос), i'=--l, 2—комплексные коэффициенты более сложного вида [5].
Для получения цифровых моделей нереализуемых аналоговых фильтров с КЧХ (17.38), (17.39) тем не менее можно использовать методы оцифровывания, рассмотренные в § 17.3, в частности, алгоритмы (17.8) (17.12), (17.19), (17.20), но с комплексными коэффициентами.
Нестационарные ЛРЗ, описываемые интегралом Дюамеля (17.4), после перехода к комплексным огибающим
(17.40)
приводят к математической модели вида рис. 17.11, б с алгоритмом
Оо
Ёи (г) = J tx (t — т) h3K (t, т) dT -о
t
= J Ёх (т) /ia„ (г, t — т) dT, где введе-
Во
на комплексная импульсная характеристика ЭЗ Лзк (/, т) h(t. т) X
X exp (— /СО ст) Лэке С- т) —
— ihaK8(t,r), также приводящая к цифровой модели комплексного фильтра рис. 17.3.
Математические модели нелинейных радиозвеньев. В РПУ приходится моделировать безынерционные нелинейные радиозвенья (БНРЗ), состоящие из последовательно соединенного БНЗ у — G (х) и так называемого формирующего звена (ФЗ). пропускающего без искажений (с единичным усилением) спектр сигнала биений на k-u гармонике (£сос) входного воздействия. Случай k —О соответствует БНРЗ типа детектора, k — 1 — БНРЗ типа нелинейных радиоусилителей или полосовых ограничителей, k > 2 — БНРЗ типа умножи-жителей частоты. В результате можно записать выходное напряжение БНРЗ в виде 
С целью нахождения явных решений для у0 (/), Eyh (t) при входном узкополосном колебании используют методы статистической радиотехники 151.
При подключении к схеме БНРЗ спереди и сзади резонансных усилителей получают структурные схемы типовых звеньев РПУ. Для их моделирования методом комплексной огибающей, очевидно, надо использовать поблочное моделирование на основе приведенного выше математического описания.
При моделировании нефункциональных инерционных нелинейных радиозвеньев пригоден лишь «метод укорочения» исходных дифференциальных уравнений, разработанный С. И. Евтяновым и Р. Л. Стратоновичем '151. Суть метода сводится к следующему.
Пусть нелинейное радиозвено описывается дифференциальным уравнением
где х = х (/, к) = Е (/, X) cos [ш0г — — гр (t, X)] — входной высокочастотный сигнал, а у (t) —выходной низкочастотный сигнал.
Тогда для получения математической модели проводим решение в несколько этапов.
Этап 1. Представляем входное воздействие х и его производные через комплексные огибающие:
(17.42)
Этап 2. Подставляя (17.42) в (17.41), получаем нелинейное дифференциальное уравнение
Этап 3. Пользуясь «медленностью» изменений комплексной огибающей Ё = Ё (t, X) и ее производных по сравнению с высокочастотным множителем exp /cor = ехр /Ф, проводим усреднение правой части полученного уравнения на интервале Ф — О — 2 я:
Дифференциальное уравнение (17.43) связывает в неявном виде все низкочастотные составляющие: входную комплексную огибающую Ё = = Ее.-№ и выходной эффект у.
Этап 4. В дальнейшем, если это необходимо, проводят укорочение дифференциального уравнения (17.43), полагая
где б — величина высокого порядка малости.
Примеры моделирования на основе принципиальных схем. Здесь для моделирования входной смеси и исследуемого радиозвена используют укороченные дифференциальные уравнения для комплексных огибающих.
Пример 17.3. Модель амплитудного диодного детектора (метод комплексной огибающей). Вернемся вновь к схеме рис. 17.7, а и перепишем дифференциальное уравнение (17.32):
(17.45)
Воспользуемся для решения методом Ван-дер-Поля.
Шаг I. Используя (17.43), усредним выражение (17.45) по фазе Ф:
T,d<y ЩШ-гР (£, у) = 0, (17.46)
где
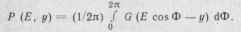
Шаг 2. Будем считать детектор линейным, введем коэффициент передачи по огибающей АГд = у!Е и крутизну вольт-амперной характеристики диода S. Тогда можно записать
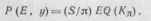(17.47)
где Q (Кя) - V\ - К\ - Кя arccos Кп -нелинейная функция.
Шаг 3. Подставив (17.47) в (17.46) и введя коэффициент нагрузки /Сн = Srln, получим окончательное решение дифференциального уравнения, связывающего низкочастотные процессы у (/) и Е (I):
t euy(t)/dt + y (t)-z(y, Е, /С„) = 0. (17.48) Здесь
z(y, Е, Кн) = KWEQ (<//£)•
Полученное уравнение соответствует модели рис. 17.13, о, где К (р) — передаточная функция rC-цепи нагрузки детектора.
Шаг 4. Проведем укорочение уравнения (17.48), положив т0(/ = 0. Тогда по-
лучим алгебраическое нелинейное уравнение
Кд-/Сн<Э(Лд) = 0.
(17.49)
Шаг 5. Вычисляя* из уравнения (17.49) коэффициенты Кд (Кн), приходим к простейшей разомкнутой модели (рис. 17.13, б):
У=Кя(Ка)Е.
(17.50)
Примеры моделирования на основе структурных схем. В [5] приведена достаточно полная библиотека моделей различных функциональных звеньев РПУ в рамках метода комплексной огибающей. Особенно просто моделируются схемы демодуляторов (детекторов), которые сводятся к простым математическим операциям над комплексной огибающей Ё --■= а — —]Ь входной смеси:
где. а — ax(t); Ь ш Ьх (t); Em Ех; Ч1 388 4\г-
Важное место занимает математическое моделирование согласованных линейных фильтров (СЛФ) с импульсной характеристикой
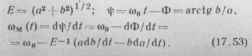
согласованной с входным сигналом
"с* (*) = Re {Ёсх (t) ехр(/сое/)}.
Тогда приходим к модели рис. 17.11, б, где следует положить
(17.52)
Пример 17.4. Математическая модель супергетеродинного РПУ с произвольной модуляцией. С помощью библиотеки моделей [5] можно «набрать» математическую модель для структурной схемы РПУ вида рис. 17. Н. Полная схема такой модели показана на рис. 17.14.
При реальном моделировании все комплексные ЛФ на рис. 17.14 можно заменять схемами вида рис. 17 .3 с расчетом ортогональных проекций а, Ь векторов смесей. Тогда переход к огибающей, фазе, мгновенной частоте должен осуществляться по формулам
Оцифровывание математической дели рис. 17.14 позволяет получить до точную эффективную цифровую мо; универсального РПУ для исследования дач помехозащищенности и помехоуе чивости.
Модель подобного вида требует бс шого разнообразия исходных данных по параметрам смеси, так и по парамет блоков РПУ.
