При построении радиоприемников двоичных сигналов необходимо обеспечить качественную работу систем автоматических регулировок и демодулятора. Особенно важны стабильность промежуточной частоты и качество формирования опорного сигнала. Так ФМн- и ОФМн-сигналы весьма критичны к сдвигам частоты. Если длительность двоичного импульса Т, а сдвиг частоты AF, то за один период двоичного сигнала накапливается фазовый сдвиг 9 = 2nAFT. Дополнительные фазовые сдвиги, вызванные нестабильностью частоты, приводят к увеличению числа ошибок. Аналогичные последствия вызывает задержка в тракте формирования опорного сигнала. Из-за ухудшения корреляции в согласованных фильтрах также увеличивается частота возникновения ошибок. Для качественной демодуляции сигнала требуется поддержание высокой степени синхронизма в ГСТС.
ГЛАВА 15
РАДИОПРИЕМНЫЕ УСТРОЙСТВА НЕПРЕРЫВНЫХ СИГНАЛОВ
§ 15.1. Общие сведения о приеме непрерывных сигналов и сообщениях
Непрерывные сигналы с амплитудной (AM) и угловой (ЧМ, ФМ) модуляциями часто применяют в системах радиовещания, связи, радиотелеметрии, телевидения и других системах передачи информации. Под непрерывными системами модуляции понимают такие, при которых информационные сообщения к (t) от первичных источников сообщения непосредственно модулируют параметры радиосигнала: амплитуду, частоту или фазу. Таким образом, информативный параметр радиосигнала является как бы аналогом информационного сообщения.
В зависимости от назначения радиосистем непрерывные сигналы могут иметь различную широкополос-ность. Последняя определяется как отношение ширины полосы промоду-лированного радиосигнала А/с к удвоенной полосе сообщения А/ч: М=-— Afr!2AFx- Так, для AM с двумя боковыми полосами широкополосность М = 1, для однополосной AM М = = 1 /2. Радиосигналы с М < 1 будем называть узкополосными, а с М > 1 — широкополосными, к которым относятся ЧМ- и ФМ-сигналы.
Широкополосность сигнала является важной характеристикой систем передачи информации, так как она показывает, какую полосу частот занимает та или иная радиосистема.
Рассмотрим краткую характеристику сообщений. Непрерывные информационные сообщения могут описываться различными функциями времени: детерминированными, выражающимися в виде полинома от времени с известными или случайными коэффициентами; случайными, с известным законом распределения или его статистическими характеристиками; суммой случайных и детерминированных функций.
В системах передачи информации непрерывное сообщение наиболее часто представляется в виде случайной функции непрерывного к (t) или дискретного к (tK) времени. Если передаваемое непрерывное сообщение имеет смысл измеренной величины (параметра), то оно описывается одномерным априорным законом распределения вероятности р (к). Если сообщение — процесс, то оно описывается многомерным априорным законом распределения вероятности рп (kj,k2,....... кп; tlt <„ tn). Следует отметить, что законы распределения сообщения р (к) иногда могут быть определены заранее по предшествующим опытам или должны априори задаваться. Если о характере сообщения ничего не известно, то наиболее целесообразно задаваться равномерным законом р(к).
Будем считать, что сообщение к (/) представляет собой реализацию нормального стационарного процесса с нулевым средним значением. Тогда исчерпывающей его характеристикой является дисперсия ajj и спектральная плотность мощности Sx (ю) или корреляционная функция Rx (т).
Удобной аппроксимацией спектров различных реальных сообщений является спектр, описываемый полиномом Баттерворта

и соответственно корреляционной функцией
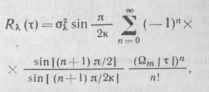
где к — степень полинома; Q,„ — максимальная частота в спектре сообщения.

где о{ == Л/я/4йт; Л\ — спектральная плотность сообщения к (/).
Из (15.1) следует, что сообщение к (t) можно рассматривать как случайное напряжение на конденсаторе интегрирующей /?С-цепи (рис. 15.1) при воздействии на ее вход напряжения белого шума (\IQ m)u\ (/), где 1/Qm = RC — постоянная времени цепи.
Процессы, описываемые спектром (корреляционной функцией) (15.1), принято называть простейшими марковскими процессами, поэтому в дальнейшем сообщение к (t) будем называть марковским информационным сообщением.
Основой синтеза оптимальных радиоприемных устройств марковских информационных сообщений, содержащихся в непрерывных радиосигналах при воздействии на приемник флуктуационных шумов, является теория оптимальной нелинейной фильтрации, рассмотренная в § 11.3.
Применительно к непрерывным сигналам задачей нелинейной фильтрации является оптимальное выделение непосредственно не наблюдаемого, а нелинейно закодированного в сигнале сообщения к (t) из совокупности полезного сигнала и шума.
Входной процесс u-z(t) представляется в виде аддитивной смеси АМ,-ЧМ- или ФМ-сигнала ыс \t, к,\, зависящего от марковского сообщения kt — к (г) и шума (/,,, (t):

(15.2)
Статистические свойства процессов к (t) и и,„ (t) предполагаются заданными. Так, марковский процесс к (t) характеризуется априори известными коэффициентами сноса a (t, kt) и диффузии Ь (г, kt), приведенными в (11.46). Тогда априорная плотность вероятности процесса к (t) удовлетворяет уравнению Фоккера — Планка — Колмогорова (11.45).
Воздействующий шум статистически независим от параметров сигнала и представляет собой нормальный стационарный белый шум с нулевым средним значением < ит (г)> = 0 и дельта-функцией корреляции
<«m(*l) "ш &) > = °-5 ^об Vl —h).
Располагая этими априорными сведениями о сигнале и шуме, необходимо решить оптимальным образом задачу выделения информационного сообщения к (/) из смеси «s (t) сигнала и шума, т. е. произвести оптимальную нелинейную фильтрацию.
Известно (см. § 11.3), что финальная апостериорная плотность вероятности параметра w(t, kt), полученная путем учета априорных плотностей вероятностей параметра и оптимальной обработки смеси их, (t) на интервале (0; 7"), определяется уравнением Стратоновича (11.47):

При условии априорного постоянства параметра к, ~ к в уравнении (15.3) следует положить a (t, kt) =
b(t, kt)~0 и тогда можно записать

(15.4)
Первые два слагаемых в правой части уравнения (15.3) учитывают изменение во времени априорной плотности вероятности (11.45), а третье — эффект уточнения априорных дан-
ных в процессе наблюдения смеси «г (/). когда случайная величина постоянна к, = к (15.4).
В соответствии с теорией нелинейной фильтрации (см.§ 11.3) оптимальный приемник должен выработать на выходе финальную апостериорную плотность вероятности W (t, kt) сообщения kt, которая получается решением уравнения оптимальной нелинейной фильтрации (15.3). Для его решения надо знать функцию / (t, kt) = d/dtlnF (kt) — производную по времени от логарифма функционала правдоподобия (11.43). При аддитивной смеси сигнала и нормального белого шума

(15.5)
— для энергетического параметра (амплитуда);

— для неэнергетического параметра (частота, фаза).
Среднее значение этой функции определено формулой (11.48).
При большом отношении сигнал/ шум финальная апостериорная плотность вероятности стремится к нормальной:

В случае квазиоптимальной фильтрации в гауссовом приближении в соответствии с формулой (11.50а) имеем такой алгоритм построения оптимальной оценки:

(15.8)

(15.9)
— постоянная во времени дисперсия апостериорного распределения, характеризующая ошибку в определении сообщения [30].
Дифференциальное уравнение (15.8) является основным алгоритмом, который в последующих параграфах будет использоваться для построения структур оптимальных и квазиоптимальных приемников непрерывных АМ-, ЧМ- и ФМ-сигналов.
В дальнейшем принят такой порядок изложения: вначале на основе теории нелинейной фильтрации находят структуры оптимальных и квазиоптимальных приемников, а затем рассматривают эвристические структуры неоптимальных приемников стандартного типа.
§ 15.2. Приемники АМ-снгнажш ^'Ш
Амплитудная модуляция широко применяется и в настоящее время, что объясняется простотой реализации всей радиосистемы и небольшой шириной спектра излучаемых колебаний.
Прежде всего поставим задачу определения структуры оптимального приемника, когда на его вход воздействует сумма полезного АМ-сигнала и флуктуационного белого шума (15.2). Задача приемника должна состоять в оптимальном выделении сообщения к (/) из входной смеси и2(0-
Полезный радиосигнал запишем в виде обычного АМ-колебания:
 (15.10)
(15.10)
Здесь А0, т,\, ш,„ ц„ амплитуда немодулированного колебания, коэффициент AM, частота и начальная
фаза соответственно, которые предполагаются известными постоянными величинами; к (/) — сообщение, представляющее собой марковский процесс, описываемый априорным стохастическим дифференциальным уравнением вида

(15.11)
где u\{t) — информационный шум типа белого с известными статистическими характеристиками <С и\ (t)> = = О, < uh ({,) Us) > = 0,5 Nk о it., /,); Л/х — спектральная плотность.
Таким образом, на входе приемника считаются известными все параметры сигнала, статистические характеристики входного и информационного шумов, а единственным неизвестным параметром является сообщение к (t).
Структуру оптимального приемника находят с помощью алгоритма (15.8). На основании априорного уравнения (15.11) коэффициент сноса
 (15.12)
(15.12)
Поскольку сообщение заложено в законе изменении амплитуды сигнала, для функции / (/, к,) следует использовать формулу (15.5), опуская члены с удвоенной частотой 2мн вследствие их фильтрации в приемнике:
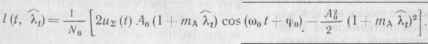
(15.13)
Производная по сообщению

Подставив (15.12) и (15.14) в (15.8), получим

X cos(w0f + <p„)— А0(1 + тА к,)].
Решая это дифференциальное уравнение, найдем исходный алгоритм для оптимальной структуры приемника:

Дисперсия апостериорного распределения определяется из выражения (15.9):

где а 1 RC Д/^— полоса частот информационного сообщения k(t).
Уравнение (15.15) моделируется когерентным (синхронным) приемником, структурная схема которого приведена на рис. 15.2. После линейного тракта, состоящего из входной цепи (ВЦ), усилителя радиочастоты (УРЧ). преобразователя частоты (ПрЧ) и уси-
лителя промежуточной частоты(УПЧ), смесь сигнала и шума (г) поступает на перемножитель (фазовый детектор), на второй вход которого от когерентного гетеродина (КГ) подается опорное колебание 2cos (со„< + ф0), частота шп и начальная фаза ср0 которого совпадают с этими же параметрами сигнала (15.10). Напряжение с выхода перемножителя, смещенное на
величину Аи (1 + m\kt), подается на усилитель с коэффициентом усиления /Сив интегрирующую /?С-цепь с постоянной времени Т. Выходное напряжение интегрирующей цепи дает
оценку сообщения kt. Полосу RC- фильтра выбирают, исходя из пропускания верхней частоты демодули-рованного сообщения и стремления пропустить как можно меньше шумов.
Рассмотренный случай, когда в принятом сигнале известны все его параметры, является идеализированным. Обычно начальная фаза ip0 в точке приема никогда не бывает известна. Более того, чаще всего она—
случайный параметр ф (t) вследствие прохождения радиоволн через канал связи. Аналитическая запись полезного радиосигнала подобна (15.10) при ф0 = ф (t). При этом условии в приемнике уже нельзя создать опорное колебание от КГ с фазой, равной фазе сигнала. Следовательно, надо искать новую структуру приемника. Постановка задачи нахождения оптимального приемника такая же, как и в первом случае. Единственное отличие состоит в том, что теперь в полезном сигнале будут два неизвестных параметра: существенный к (t) и несущественный ф (t).
Исходный алгоритм стационарной фильтрации (15.8) запишем для двух случайных параметров.
Для информационного сообщения
 (15.16)
(15.16)
Для случайной фазы, в предположении ее равновероятности в пределах — я. < ф < л, коэффициент сноса а (ф() — 0. Тогда
 (15.17)
(15.17)
где |  —апосте-
—апосте-
риорная дисперсия оценки фазы
ф (t). Здесь было учтено, что случайные процессы а (г) и ф (t) статистически независимы, поэтому их взаимно-корреляционная функция оценок равна нулю.
Ч
Для производной dl (г, kt)! dkt можно воспользоваться формулой (15.14), подставив ф0 == <р (/). Производную этой функции по фазе находят из (15.13).

Подставим (15.14) в (15.16) и (15.18) в (15.17), а затем решим эти уравнения относительно параметров

С помощью этих двух уравнений можно построить структурную схему оптимального приемника, осуществляющего квазикогерентный прием
АМ-сигнала (рис. 15.3). Уравнением (15.19) моделируется информационный канал приемника, который подобен каналу в когерентном приемнике (см. рис. 15.2)- Отличие состоит в том, что в схеме рис. 15.3 опорное напряжение на неремножитель (фазовый детектор) информационного канала подается от системы ФАПЧ. которая моделируется уравнением (15.20). Система ФАПЧ здесь используется как следящий фильтр (см. § 10.4).
На перемножитель этой системы подаются колебания входной смеси us (t) и перестраиваемого гетеродина (ПГ), который вследствие обратной связи синхронизируется приходящим сигналом. В режиме захвата частота ПГ совпадает с частотой полезного сигнала, а значение фазы соответствует
ее оценке ф. Так как оценка фазы, выработанная в системе ФАПЧ, никогда не совпадает с фазой входного сигнала ср (t), то и опорный сигнал на иеремножителе от ПГ не является точной копией полезного сигнала. Поэтому такой приемник называется квазикогерентным.
Заметим также, что на усилитель системы ФАПЧ воздействует напря-
жение АРУ вида Л„ (1 + mAXt). Еще одной особенностью системы является зависимость усилителей в информационном канале и системы ФАПЧ от спектральной плотности входного шума N„. Поэтому если величина N0 неизвестна или изменяется во времени, то ее необходимо измерять.
Подчеркнем, что в рассмотренных случаях когерентного и квазикогерентного приемников при демодуляции АМ-сигнала используется информация о фазе сигнала: в первом случае — точно известная начальная фаза ф0, во втором — оценочные значения ф'
На практике иногда применяют двухполосную AM без несущей частоты, поскольку в последней не содержится полезной информации. Запись двухполосного АМ-сигнала без несущей подобна (15.10), только в амплитуде сигнала слагаемое «1» полагается равным нулю. В последующих уравнениях, начиная с (15.13), где ветре-
чаются слагаемые вида (1 -f гпА ^<)> надо полагать 1 == 0. Структуру оптимального приемника для такого сигнала строят по уравнениям (15.19), (15.20) с выполнением указанного условия. Тогда структурная схема оптимального приемника двухполосной AM без несущей подобна рис. 15.3 с одним изменением: в цепи обратной связи от информационного канала отсутствует сумматор с Л 0, поэтому сиг-
налом АРУ будет А„ тА X,.
Рассмотрим вариант некогерентного приемника АМ-сигналов, когда информация о фазе полезного сигнала не используется (рис. 15.4). В качестве демодулятора применяется амплитудный детектор (АД), выделяющий огибающую суммарного колебания сигнала и шума. Структура стандарт-
ного приемника АМ-сигналов изображена с цепями АРУ, которые включают детектор Дару, фильтр Фару и регулируют усиление по каналам УРЧ, УПЧ. Кроме того, показана система АПЧ гетеродина (Г), состоящая из частотного дискриминатора ЧД, фильтра ФАпч и управляющего элемента УЭ.
Известно, что преобразования сигнала и шума в АД (см. § 7.2) происходят иначе, чем в ФД (перемножителе, § 7.4). На выходе АД образуется спектр биений между частотами сигнала и шума, а в ФД этого эффекта нет. Поэтому целесообразно рассмотреть вопрос о соотношениях сигнала к шуму на выходах когерентного (синхронного) и некогерентного амплитудных детекторов, имея в виду,что это соотношение определяет помехоустойчивость соответствующих видов приемников.
В когерентном приемнике (см. рис. 15.2) на входе ФД (перемножителя) информационного канала отношение средней мощности АМ-сигнала к мощности шума определяется соотношением

ется из (15.10); о% — дисперсия случайного сообщения X (/); jV0 — спектральная плотность шума, которая считается симметричной относительно частоты со,,; А Г*. — полоса информационного сообщения.
На выходе ФД, полагая его коэффициент преобразования К фд 1. имеем

Высокочастотные составляющие напряжения «фд далее отфильтровываются, поэтому низкочастотное напряжение

(15.23)
Первый член — полезный сигнал, второй — шум. Определим из (15.23) отношение средней мощности сигнала к шуму на выходе когерентного детектора (КД).
Средняя мощность сигнала

Этот результат справедлив независимо от того, является ли фаза сигнала случайной <р (г) или детерминированной ф„ величиной,так как разность фаз (ц(. — ф ш) всегда сл учайная и среднее от cos'2 (ф(. — фш) 2.
Отношение сигнал/шум на выходе КД когерентного и квазикогерентного приемников
 (15.24)
(15.24)
Сравнивая ^вЫХ (15.24) с цяХ (15.21), замечаем, что
 т. е. на выходе когерентного и квазикогерентного приемников отношение сигнал/шум линейно зависит от такого же отношения на входе. Это свойство оптимальных приемников является решающим для помехоустойчивости.
т. е. на выходе когерентного и квазикогерентного приемников отношение сигнал/шум линейно зависит от такого же отношения на входе. Это свойство оптимальных приемников является решающим для помехоустойчивости.
В некогерентном приемнике (см. рис. 15.4) отношение сигнал шум на входе АД определяется по-прежнему формулой (15.21). Считая характеристику АД квадратичной (ыВЫ\ = /Сд«в\), получим
МА Д(/)=1 "с(/. Х,)+"ш(/)12.
С учетом последующей фильтрации высокочастотных составляющих можно записать

Средняя мощность сигнала на выходе АД (Яс)вых = Л40 0 + т£а£)2/4. Дисперсия шума на выходе квадратичного детектора 
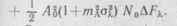
Отношение сигнал/шум на выходе АД

Используя значения qbMX (15.25) для когерентного и (15.27) для амплитудного детекторов, можно оценить выигрыш когерентного приема по сравнению с некогерентным: (</вЬ1Х)кд/ %вых)ад 2 (i /qax + 1), откуда следует, что при £/вх > 1 выигрыш стремится к двум, а более существенный выигрыш получается при qBX <^ 1. Эти выводы показывают, какие типы приемников (демодуляторов) необхо-
димо проектировать при различных отношениях сигнал/шум на входе приемников, которые должны предварительно определяться при расчете линии передачи радиосистемы.
§ 15.3. Прохождение АМ-сигнала через линейную часть приемника
При прохождении АМ-сигнала через линейную часть приемника (до демодулятора) возникают линейные и нелинейные искажения передаваемых сообщений.
Вначале рассмотрим линейные искажения. Пусть на вход приемника подается АМ-сигнал с частотой сообщения Q 2nF:

(15.28)
Передаточную функцию линейного тракта приемника обозначим через К (/со) К (со) ехр [— /ср (со)|, где К (со), ср (со) амплитудно-частотная (АЧХ) и фазочастотная (ФЧХ) характеристики соответственно.
Если АЧХ и ФЧХ симметричны относительно средней частоты со0 и при точной настройке приемника на частоту сигнала (со,, = сос), то АМ-сигнал на выходе линейного тракта (рис. 15.5) в стационарном режиме можно представить в виде

(15.29)
где у (со) = К (со)//Сп — нормированная АЧХ, а Ко — коэффициент усиления на частоте со0.
Из (15.29) следует, что глубина модуляции на выходе уменьшается до величины у (to) тА и огибающая получает дополнительный фазовый сдвиг ф (w).
Если сигнал (15.29) представить в виде спектра, то боковые составляющие сигнала на частотах ыс ± £1 будут иметь амплитуды К0АоУ (шо ± ±Q) mA/2 и фазы =Рф (w0 ± Q), отличающиеся от соответствующих величин входного сигнала (15.28). Эти изменения представляют собой л и-нейные частотные искажения передаваемого сообщения Q, которые выявляются на выходе амплитудного детектора приемника.
Полученные результаты для тональной модуляции нетрудно обобщить на случай сложного сообщения, состоящего из разных частот.
Рассмотрим теперь неточную настройку приемника на несущую частоту АМ-сигнала (ы0 Ф ыс), показанную на рис. 15.6. Можно заметить, что усиление боковых частот здесь разное, т. е. возникает их асимметрия. Если представить АМ-колебание в виде векторной диаграммы с неравными боковыми составляющими (рис. 15.7), то видно, что суммарный вектор АМ-колебания ОР описывает во времени сложную огибающую, отличающуюся от гармонической (15.28). Кроме того, появляется паразитная фазовая модуляция в (г). Искажение формы огибающей свидетельствует о появлении в ее спектре новых частот, кратных частоте Q полезной модуляции. Выявим эти паразитные частоты.
В стационарном режиме на выходе линейного тракта получается напряжение

Амплитуда этого напряжения

После разложения в степенной ряд с учетом первых двух членов имеем
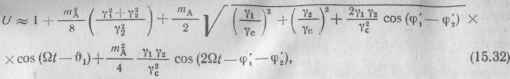
где

Из формулы (15.32) следует, что в результате нарушения симметрии амплитуд и фаз колебаний боковых частот возникают нелинейные искажения передаваемых сообщений. Они проявляются в возникновении второй гармоники сообщения 2Й, которая образуется на выходе амплитудного детектора. Если бы в разложении квадратного корня (15.31) учитывались третий и последующие члены, то возникали новые гармоники частоты сообщения nil.
Уменьшение нелинейных искажений достигается возможно более точной настройкой приемника (со,,) на несущую частоту сигнала <ос, т. е. выполнением условия (о0 = шс.
Еще одной существенной причиной нелинейных эффектов в линейной части приемника АМ-сигналов является нелинейность вольт-амперных характеристик активных приборов, которая при больших уровнях полезного сигнала в основном канале или помехи в соседнем канале приводит к интермодуляции, перекрестным искажениям, блокированию, а также сжатию амплитуды полезного сигнала в приемнике (см. § 1.3).
Интермодуляция возникает за счет нелинейных свойств высокочастотных каскадов до УПЧ благодаря взаимодействию двух и более помехо-вых сигналов и их гармоник. При этом частоты помеховых сигналов сопх не совпадают с частотами основного сос и побочных каналов приема радиоприемника и могут проникать в УПЧ как при наличии, так и в отсутствие полезного сигнала.
Если ограничиться двумя помехо-выми сигналами с частотами сопх|
и о)пх2, то из-за нелинейности высокочастотного тракта возникают помехи на частотах сопх = пшпх1 ± mtonx2, где п, т = О, 1, 2,... Если частота сопх равна или близка к частоте сигнала (ос, либо побочных каналов приема, то она не может быть отфильтрована в УПЧ и после детектирования спектр помеховой модуляции будет искажать спектр полезной информации.






