Методика решения подобной дискретной задачи сводится к использованию общих байесовых решений с применением классических методов теории вероятностей [81 перехода от непрерывных случайных величин к дискретным. Здесь оптимальный Прм многоканален и в качестве выходных эффектов формирует апостериорную вероятностную функцию для всех возможных исходных ситуаций:
(1 1.4)
где Pi = Р (к = j) — априорная вероятностная функция, a Lt (X) = — р (Х/Х = /) — функция правдоподобия.
Решающее устройство для одного из частных критериев оптимальности в качестве решения D = Dj принимает ту гипотезу, для которой выходной эффект оптимального Прм ppsJ (X) максимален 130]. При таком решении минимизируется средняя вероятность (по всем гипотезам)
ошибочных решений min {Pou,x —
М
= min { v р.р (D = j/k = /)}.
i = i
3. Оптимальные РПУ бинарного различения. При М — 2 из предыдущих решений имеем частный случай бинарного различения, определяющий структурные схемы РПУ в системах радиосвязи с дискретными двоичными сигналами (см. гл. 15). Здесь алгоритмы принятия оптимального бинарного решения D = Dj, j— 1, 2, упрощаются [30]. Оптимальный Прм в качестве выходного эффекта формирует отношение правдоподобия Л2, и сравнивает его в РУ с некоторым пороговым уровнем Л, зависящим от априорных вероятностей Pi в формуле (11.4) и некоторых назначаемых относительно произвольно весовых коэффициентов (функций потерь). Алгоритм оптимального бинарного различения принимает вид
В этом случае РУ (рис. 11.1) пре вращается в пороговый каскад.
4. Оптимальные Р П 5 бинарного обнаруже
н и я, Бинарный обнаружитель мож но рассматривать как частный случа] бинарного различения, если ситуа пню к 2 заменить ситуацией при
2К
сутствия сигнала в наблюдаемом процессе (Я, = 1 или ДА), а ситуацию % = 1 — ситуацией отсутствия сигнала (к = 0 или НЕТ). Структурная схема оптимального РПУ при этом остается прежней. Как показано на рис. 11.3, она состоит из оптимального Прм, вырабатывающего отношение правдоподобия Л (X), и решающего устройства (РУ) в виде порогового каскада (ПК) с пороговым уровнем h0.
Алгоритм оптимального бинарного обнаружения принимает вид
Величина порогового уровня h0 зависит [301 от априорных вероятностей присутствия или отсутствия сигнала в смеси (11.1), а также от выбранного критерия оптимальности, например критерия Неймана — Пирсона. В этом частном случае максимизируется вероятность правильного обнаружения сигнала в смеси при фиксированном уровне ложной тревоги.
Методы устранения априорной неопределенности. Адаптивный прием. Байесов подход, являющийся наилучшим в теории оптимального приема, требует полной априорной определенности, т. е. точного значения в формуле (11.2): априорной плотности вероятности параметра р (к); функции правдоподобия' L(k) = р (Х /л).
Подобная полная априорная определенность часто отсутствует, что не позволяет применить байесов подход к синтезу оптимального приемника. Существует ряд методов у стране-чия априорной неопределенности.
Случай 1. Параметрическая априорная не-
определенность. В этом случае плотности вероятностей р (к), р (Х /к) в формуле Байеса (11.2) определены в точностью до нескольких статистических параметров.
При несущественной параметрической неопределенности для ее устранения считают, что одна или обе плотности вероятностей зависят также от несущественного (мешающего) параметра а с заданным законом распределения р (а/к). Тогда в формулу Байеса (11.2) подставляют усредненные (по несущественному параметру а) значения рср (к) и Lcp (к), как показано в § 11.2.
Если статистика параметра а неизвестна (существенная параметрическая неопределенность), прибегают к косвенным методам ее нахождения, в частности, к обучающим выборкам. Это приводит к адаптивным методам приема.
Случай 2. Не параметрическая априорная неопределенность. В этом случае функция правдоподобия L (к) обычно известна точно, а функция р (к) — неизвестна вообще. Для устранения подобной априорной неопределенности прибегают к различным способам.
Если апостериорная точность оценки значительно выше априорной, то можно воспользоваться формулой (11.3) и применить критерий максимума правдоподобия.
В ряде случаев применяют минимаксный подход, когда ищут байесо-во решение (по критерию минимума среднего риска) для наименее предпочтительного априорного распределения, при котором минимальный средний риск максимален.
В случае незнания функции р (к) можно также применить критерий минимума условного риска, когда функция потерь g (и, k, X), где и - D — решение; к — оцениваемый параметр; X — выборка входной смеси, усредняется лишь по параметрам и и X:
min {г c., (Фо, к)} = min { I g (ы, X, X) ■ X q(l(u/X )/7 (XA)d«dX}.
Здесь фо = фо (ы/Х) - решающее правило.
Случай 3. Применение адаптивного подхода при с ил ьной априорной неопределенности. Если плотности вероятностей р (к), Р (Х /к) неизвестны и аналитические методы устранения априорной неопределенности затруднительны, прибегают к методам адаптивного приема. В этих случаях с помощью обучающих выборок входной смеси (X =
Х /к), в которой закодирован процесс к - к (t), пытаются получить эмпирически необходимую статистику:
для определения оценок плотностей
вероятностей р (к), L (к);
для формирования среднего или апостериорного риска г (и, X) = =.'J g(u, к, X )p(k,'X )dk;
для уточнения структуры решающего правила к (ы/Х).
При этом для устранения априорной неопределенности применяют адаптивный байесов подход, когда в формуле (11.2), например, фигурируют экспериментальные оценки р (к), L(k).
§ 11.2. Оптимальный радиоприем в аддитивном гауссовом белом шуме
Постановка задачи. Рассмотрим частный случай оптимального приема при следующих исходных условиях.
В наблюдаемом аддитивном процессе (11.1) сигнал считаем узкополосным квазигармоническим, зависящим как от существенного параметра к, подлежащего оценке, так и от несущественного параметра а:
Здесь Л0 = У2ЯС — энергетический параметр, а /0, /\д, т, ф„—неэнергетические параметры (несущая частота /0, доплеровский сдвиг частоты F%, групповая задержка т, начальная фаза фо).
Распределение этих параметров по существенным и несущественным зависит от конкретной постановки задачи. Во всех случаях комплексная огибающая Е (t) = U (t) ехр [— /ф (t)] считается точно известной.
Шум иш (г) в смеси (11.1) считается гауссовым белым шумом. Это соответствует модели случайного б-корре-лированного процесса с односторонней спектральной плотностью Nn и статистическими характеристиками:
Если сигнал зависит и от несущественного параметра а, будем считать известной условную плотность вероятностей р (а/к). Это позволяет устранить подобную несущественную априорную неопределенность путем вычисления усредненной по несущественному параметру функции правдоподобия:
(11.9)
Задача состоит в нахождении конкретной структуры оптимального Прм (см. рис. 11.1). Для решения поставленной задачи необходимо найти выходной эффект z оптимального Прм, в качестве которого при гауссовых шумах обычно берут монотонные (логарифмические) функции от апостериорной плотности вероятностей pps (к) или функции правдоподобия L (к)-
1. Оптимальный приемник оценки параметра сигнала. Найдем функцию
Правдоподобия L (л) для аддитивной смеси (11.1). Когда сигнал ис (/, X) известен точно, достаточно воспользоваться правилом пересчета плотностей вероятностей [8]:
Ml.10)
где иш, Uc (к), X — m-мерные векторные выборки (на интервале наблюдения Т = mAt) случайных процессов иш (/), «с (/, к), X (t) Uv (t),
соответственно.
Используя (11.8), (11.10), находим
В результате предельного перехода Лг->0, mAt Т находим функционал правдоподобия
(11.11)
где с = lim cm — некоторый неопре-
Дг-+0
деленный коэффициент, не зависящий от X. и не влияющий на оценку.
Проводя под интегралом в (1111) необходимые преобразования и перенося все члены, не зависящие от к, в коэффициент г', получим
(11.12) Здесь
— энергетическое отношение сигнал шум;
— корреляционный интеграл.
Найдем также усредненные функционалы правдоподобия, получаемые из (11.9) предельным переходом:
(11.15)
где § (к, се) ■- р \х (/) к, а\ — не-усредненный функционал правдоподобия для сигнала и,. (/, к, а) с несущественным параметром а.
Рассмотрим два типа таких сигналов.
Сигнал с неизвестной начальной фазой и точно известной амплитудой. Часто в сигнале (11.7) начальная фаза <|„ либо неизвестна, либо равновероятно флуктуирует в пределах |ср„|<: л, а амплитуда А„ — постоянна и точно известна. Тогда следует положить а <р0, р (а X)
р (ц„к) 12л, |ср|<л и считать неэнергетический параметр k — f/0. F;x, т| подлежащим оценке. Заменив в (11,12) — (11.14) сигнал
(/, X) на сигнал ис (/, X, а ц„) и используя (11.7), найдем неусред-ненный функционал правдоподобия:
фективная длительность сигнала uc(t, X, а) на интервале наблюдения и введены функции
выражаемые через корреляционные интегралы
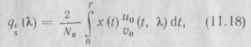
формируемые с помощью двух ортогональных опорных напряжений
Усредняя (11.16) по равновероятной фазе, в соответствии с (11.15) найдем усредненный функционал правдоподобия:
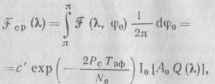
(11.20)
где I„ (z) модифицированная функция Бесселя.
Сигнал с неизвестной начальной фазой и флуктуирующей амплитудой. Если фаза ф0 неизвестна или флуктуирует, а амплитуда А„ независимо флуктуирует по закону Рэ-лея, то следует положить а = [А0,
Ф„1, р (а/%) = р (А„) р (фо) - -А- х
;- exp f— tj^ J, где Р0 — средняя
мощность флуктуирующего сигнала. В этом случае вместо (11.15) можно получить [301 другое решение для среднего функционала правдоподобия:
Здесь, <70 щ РоГзф/Л'о - 9 C.CD/N0 — энергетическое отношение сигнал/ шум,a Q (к) — та же функция (11.17).
Структур.а оптимального приемника оценки параметра сигнала, из-
вестного точно. Методика решения задачи сводится к проведению следующих математических операций.
Зная функцию правдоподобия L (к) по формуле Байеса (11.2), находим апостериорную плотность вероятностей р (к!\) и в качестве вы-
ходного эффекта оптимального Прм, как говорилось выше, берем ее логарифм z (к) = \пр(к X) = In/г -4-+ In р (к) + In L (к).
Ограничившись случаем высоко точных апостериорных оценок, с учетом (11.3) представим выходной эффект в виде
(11.21)
В дальнейшем рассмотрим лишь случай аналоговой обработки. Тогда путем предельного перехода Л/ -+ 0 из (11.21) находим выходной эффект оптимального приемника
z (к) я» In,f (к) «— u- (fc) 4- </ (>.).(11.22)
Здесь р (к), q (к) определены формулами (11.13), (11.14), а сигнал нсХ х(/, к) — формулой (11.7), где к =
= Ы о, /о. ^д. Фо. т1-
Структурная схема оптимального Прм, называемого корреляционным, реализующая алгоритмы (11.22), (11.13), (11.14), показана на рис. 114. Она является конкретизацией общей схемы оптимального Прм рис. 11.1 для частного случая аддитивного гауссова белого шума. Выходной эф-
фект намного проще, чем в общем байе-совом решении, и формируется коррелятором, состоящим из перемножителя и интегратора. Первый производит перемножение смеси (11.1) с когерентным опорным сигналом и0 (t)= = ис (t, X), совпадающим с точной копией сигнала, содержащегося во вход- (-ной смеси. Интегратор с весовым множителем 2/Л/0 вырабатывает корреляционный интеграл (11.14). Для формирования выходного эффекта к нему требуется добавить энергетический параметр (11.13). Оптимальный Прм рис. 11.4 для сигнала, известного точно, называется также когерентным, так как он реализует когерентную свертку входной смеси с когерентным по сигналу опорным напряжением.
В частном случае оценки неэнергетического параметра X = [/„, /\д, ф0, т), когда параметр' А0 считается точно известным, из (11.13) находим постоянный (не зависящий от X) параметр р (X) — р = Рс Tai)!N0. При этом выходной эффект оптимального Прм
(11.22а)
Эта схема оценки отличается от схемы рис. 11.4 отсутствием выходного сумматора.
В другом частном случае оценки лишь амплитуды Ай при модели входного сигнала (11.7) вида ис (t, X = '«= А0) = А0 ufN (0 = Л0 и (t) х Xcos [2n/0/ — ф(/) — ф0] оптимальный
Прм сразу выносит оценку А„ =
2 J
= — J x'(t) ucN U) dt, где Гэф =
1 ЭФ о
Т
— \ uIn (t)dt. При этом решающего о
устройства не требуется и все РПУ является линейным коррелятором.
Структура оптимального приемника оценки параметра сигнала с неизвестной начальной
фазой и известной амплитудой. Рассмотрим частный случай оценки неэнергетического параметра X = |/0, Ря, т) сигнала с неизвестной начальной фазой ф0 и точно известной амплитудой А0 —- = У2РС. В качестве выходного эффекта оптимального Прм вместо
(11 .22) возьмем логарифм усредненного функционала правдоподобия (11 .20). Тогда получим
z(X) = \n.fcp (Х) = \п I0[/10Q (>.)],
(11 .23)
где Q (X) определено формулами (11.17) — (11.19).
Структурная схема так называемого квадратурного корреляционного оптимального приемника, реализующего алгоритмы (11.7) — (11.9), (11 .23), приведена на рис. 11.5. Приемник состоит из двух квадратурных корреляторов вида рис. 11.4, работающих от двух ортогональных опорных сигналов Аои0 (/, X), Anv„ (t, X), определяемых формулой (11.19). В результате формируются корреляционные интегралы A0qc (X), A„qs (X), определяемые формулой (11.18). Для формирования выходного эффекта
(11 .23) служит безынерционный нелинейный преобразователь, который с помощью двух квадраторов, сумматора и первого нелинейного элемента (НЭ,) формирует по формуле (11.17) функцию А0 Q (X). Второй нелинейный элемент (НЭ2) с характеристикой г = In 10 (•) создает на выходе оптимального Прм нужный сигнал. По причинам, указанным ниже, оптимальный Прм рис. 11.5 называется некогерентным.
Структура оптимального приемника оценки параметра сигнала с неизвестной начальной фазой и флуктуирующей амплитудой. Рассмотрим частный случай оценки неэнергетического параметра X — 1/0, F д, т) сигнала, начальная фаза которого не--известна, а амплитуда А„ флуктуирует по закону Рэлея. При этом в со-
ответствии с формулой (11.20а) выходной эффект оптимального Прм
(11. 24)
где <7в, Тдф — известные параметры, а Q (К) — функция (11.17).
Алгоритмам (11.24), (11.17) — (11.19) соответствует структурная схема оптимального приемника рис. 11.6. Она несколько отличается от схемы рис. 11.5 (безынерционным нелинейным преобразователем и нормировкой в опорных сигналах). Однако основная операция, осуществляемая квадратурными корреляторами, остается.
2. Оптимальный приемник многоальтернативного различения. Конкретизируем общую схему рис. 11.1 для задачи многоальтернативного различения сигналов ис (t, X i) — uci (/), известных точно, в аддитивном гауссовом белом шуме при простой функции потерь. В соответствии с общим решением (11.4) выходной эффект t'-ro канала многоканального оптимального Прм при аналоговой обработке zt = z(k - i) = kpifi \x (01, где.f t \x (01 -- p \x (t)IX — i] — функцио-
нал правдоподобия для i'-й ситуации. Используя решения (11.12)— (11.14) и взяв в качестве выходного эффекта логарифмическую функцию zt = In {kiptft \х (t)]}, при дополнительном допущении одинаковости априорных вероятностей р-, для всех ситуаций можно записать
(11.25)
Структурная схема оптимального РПУ состоит из многоканального корреляционного Прм, формирующего выходные эффекты (11.25), и РУ, выбирающего для оценки и = i канал с максимальным выходом Z; max.
3. Оптимальный приемник бинарного различения и обнаружения. Конкретизируем общую структуру оптимального Прм (см. рис. 11.1, 11.3) для частного случая бинарного различения в гауссовом белом шуме одного из двух сигналов ыс, (/), ис2 (0. известных точно. В качестве выходного эффекта оптимального Прм возьмем логарифм отношения правдоподобия
(11.5), который при аналоговой обработке переходит в логарифм функционала отношения правдоподобия z = In {/21 \x(t)\) Hm {In Л21Х
X (X)} =- In {§, \x{t )\l$l \х (/)!}• Используя выражения (11.12) — (11.14), (11.25), (11.5), найдем искомое решение для алгоритма бинарного различения:
Здесь
(11.27)
— пороговый уровень в РУ, с которым сравнивается (в момент времени I Т) выходной эффект оптимального Прм. В случае превышения этого порога (2 >/illop) принимается гипотеза о присутствии в смеси (11.1) второго сигнала. В противном случае (z<Zhnop) принимается первая гипотеза.
Структурная схема оптимального приемника бинарного различения показана на рис. 11.7. Он состоит из двухканального коррелятора (см. рис. 11.4) с опорными напряжениями в виде копий обоих сигналов ucl(t), ис2 (0 и разностного устройства. Ре-
шающее устройство вырождается в пороговый каскад с порогом (11.27).
При бинарном различении флуктуирующих сигналов, модели которых были рассмотрены выше, выход оптимального Прм соответствует разности z = 22 — Zj, где Zi следует брать в виде решения (11.23) или (11.24). Это означает, что структурная схема оптимального Прм при флуктуирующих сигналах также двух-канальна, но каждый из каналов имеет схему квадратурного коррелятора вида рис. 11.5, 11.6.
Структурные схемы и алгоритмы оптимальных РПУ бинарного обнаружения сигнала легко получаются из соответствующих алгоритмов бинарного различения путем замены индексов в соответствии с методикой, рассмотренной в § 11.1. Так, при бинарном обнаружении сигнала, известного точно, из (11.6) путем предельного перехода получаем алгоритм
Структурная схема такого бинарного обнаружителя представляет собой соединение оптимального корреляционного Прм рис. 11.4 (без сумматора на выходе) и РУ в виде порогового каскада с порогом (11.29)."
При бинарном обнаружении флуктуирующих сигналов рассмотренных типов алгоритмы имеют вид
где Q — Q (к) вычисляется по формулам (11.17) — (11.19).
Структурная схема бинарного обнаружителя в этих случаях соответствует схемам оптимальных Прм рис. 11.5, 11.6 в соединении с РУ в виде порогового каскада.
4. Особенности оптимальных приемников. При реализации корреляционных приемников рис. 11.4, когда сигнал известен точно, возникает проблема опорного сигнала «п (/) — где взять нужную копию входного сигнала ис (/, к), который принимается вместе с шумом и в отдельном виде не фиксируется. Здесь возможны следующие частные случаи.
В однопозиционной радиолокации, когда передатчик и приемник пространственно совмещены, когерентный опорный сигнал может быть легко получен из излучаемого сигнала. Это по существу когерентный (синхронный) прием, как того требует структура оптимальных Прм вида рис. 11.4.
В многопозиционной радиолокации, радиосвязи и ряде других случаев, когда передающий и приемный пункты пространственно разнесены, создать в корреляционном Прм опорное напряжение, когерентное излучаемому сигналу, не представляется возможным. Здесь приходится переходить к квазикогерентному приему, когда опорный сигнал не является точной копией входного сигнала. Имеется ряд способов создания опорного сигнала при квазикогерентном приеме путем введения в схемы корреляционных приемников капала опорного сигнала (канала синхронизации). Первый способ — ввод высокостабильного генератора опорного напряжения (ГОН) с периодической
подстройкой по каналу синхронизации
от других средств. Второй способ — выделение опорного сигнала из входной смеси ms (/) путем фильтрации сигнала в следящих схемах типа ФАП и т. д. При этом опорный сигнал содержит остаточные шумы, ухудшающие качества оптимального приема. Третий способ — отказ от фильтрации входного сигнала от шумов и принятие в качестве опорного сигнала самой входной смеси (с дополнительным сдвигом по групповой задержке т). Это по существу метод автокорреляционного приема, когда на выходе коррелятора рис. 11.4 вместо выходного эффекта (11.14) создается эффект в виде корреляционной функции входной смеси 
X dt -f шумовые 
составляющие. В этом случае уровень шумовых составляющих, вызванный биениями типов сигнал — шум, шум — шум, значительно выше, чем в оптимальном Прм рис. 11.4 с чистым опорным сигналом (без шумов). Наконец, существуют способы подбора опорного сигнала (форма которого известна) по параметру к, диапазон которого при приеме (Лш)п — к max) заранее известен. При этом возможен многоканальный (параллельный) корреляционный приемник с фиксированными опорными сигналами ucj (t, kj), где kt - kmin г /АХ, и одноканаль-ный приемник с опорным сигналом ис \ t, к (t)\. у которого параметр к (/) последовательно изменяется во времени от кт1п яок,пях.
Вместо коррелятора рис. 11.4 можно применить согласованный фильтр (СФ). Рассмотрим этот вопрос подробнее.
Выходной эффект коррелятора можно записать в виде сигнальной и шумовой составляющих:
Альтернативой коррелятора служит СФ 130], имеющий импульсную характеристику h (t, к) = ис (/„ — — 1,к), согласованную с опорным сигналом ис (t, X). Выходной эффект СФ также состоит из сигнальной и шумовой составляющих:
(11.31)
Выходные эффекты коррелятора (11.30) и СФ (11.31) существенно различаются как по сигналу, так и по шуму. Так, выходной эфффект СФ носит высокочастотный характер с ярко выраженной огибающей, а у коррелятора он имеет вид нарастающего постоянного напряжения. Однако коррелятор и СФ можно сделать адекватными, если напряжение с выхода СФ снимать ключом в момент времени t = Т и потребовать равенства сигнальных составляющих:
