Уравнение Колмогорова — Чепмена

Уравнение Колмогорова — Чепмена для однопараметрического семейства непрерывных линейных операторов P (t)   » t> 0в топологическом векторном пространстве выражает полугрупповое свойство:

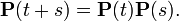
Чаще всего этот термин используется в теории однородных марковскихслучайных процессов, где P (t)  — оператор, преобразующий распределение вероятностей в начальный момент времени в распределение вероятности в момент времени t (P (0)=1).

Для неоднородных процессов рассматриваются двухпараметрические семейства операторов  t > 0» />, преобразующих распределение вероятностей в момент времени t > 0в распределение вероятности в момент времени h > t > 0. Для них уравнение Колмогорова—Чепмена имеет вид

 h > t > 0.» />

Для систем с дискретным временем параметры t, h, s принимаютнатуральные значения.

Прямое и обратное уравнения Колмогорова

Формально дифференцируя уравнение Колмогорова—Чепмена по s при s = 0 получаем прямое уравнение Колмогорова:

где

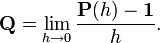
Формально дифференцируя уравнение Колмогорова — Чепмена по t при t = 0 получаем обратное уравнение Колмогорова

Необходимо подчеркнуть, что для бесконечномерных пространств оператор Q уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.

Примеры

Рассмотрим однородные марковские случайные процессы в R ⁿ для которых оператор переходных вероятностей P (t) задаётся переходной плотностью p (t, x, y): вероятность перехода из области U в область W за время t есть . Уравнение Колмогорова—Чепмена для плотностей имеет вид:

При 0, \, t \to 0″ /> переходная плотность p (t, x, y) стремится к δ-функции (в смысле слабого предела обобщенных функций): . Это означает, что  Пусть существует предел (также обобщённая функция)

Тогда оператор  действует на функции f (x), определённые на как  и прямое уравнение Колмогорова принимает вид

а обратное уравнение Колмогорова

Пусть оператор  — дифференциальный оператор второго порядка с непрерывными коэффициентами:

(это означает, что q (x, y) есть линейная комбинация первых и вторых производных δ(x − y) с непрерывными коэффициентами). Матрица aij симметрична. Пусть она положительно определена в каждой точке (диффузия). Прямое уравнение Колмогорова имеет вид

Это уравнение называется уравнением Фоккера — Планка. Вектор bj в физической литературе называется вектором сноса, а матрица aij —тензором диффузии Обратное уравнение Колмогорова в этом случае

Модели СМО, описываемые типа «гибель и размножение», их характеристики

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов – так называемый процесс гибели и размножения.

Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис.1:

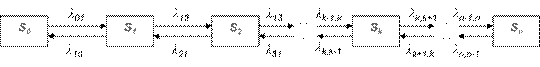Рассмотрим упорядоченное множество состояний системы:

S₀, S₁, S₂, …, S_k.

Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния S_k возможны переходы только в состояние S_k-1, либо в состояние S_k+1.* (При анализе численности популяций считают, что состояние S_k соответствует численности популяции равной k, и переход системы из состояния S_k в состояние S_k+1 происходит при рождении одного члена популяции, а переход в состояние S_k-1 – при гибели одного члена популяции.)

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями λ_k,k+1 или λ_k+1,k.

По графу, представленному на рис. 1, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений получим:

для состояния S₀

λ₀₁ p₀ = λ₁₀ p₁      (1)

для состояния S₁ – (λ₁₂ + λ₁₀) p₁ = λ₀₁ p₀ + λ₂₁ p₂, которое с учетом (1) приводится к виду

λ₁₂ p₁ = λ₂₁ p₂      (2)

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

λ₀₁ p₁ = λ₁₀ p₂

λ₁₂ p₁ = λ₂₁ p₂

……………….

λ_k-1,k p_k-1 = λ_k,k-1 p_k

λ_n-1,n p_n-1 = λ_n,n-1 p_n

к которой добавляется нормировочное условие

p₀ + p₁ + p₂ + …+p_n = 1.        (4)

Решая систему (3), (4), можно получить:

Подставляя p1, p2,.., pn в нормировочное условие, получим:

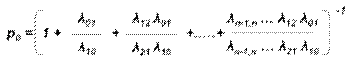
Легко заметить, что в формулах (5) для p1, p2,…,  pn коэффициенты при p0 есть слагаемые, стоящие после единицы в формуле (6). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния S_k (k=1, 2, …, n), а знаменатели – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния S_k