Пуассоновский процесс
В п.4.3 главы 1 мы рассматривали пуассоновский процесс как частный случай процесса с независимыми приращениями, который обладает следующими свойствами
1) 
;
2) 
случайные величины 
являются независимыми;
3) 
.
Покажем, что этот процесс можно рассматривать и как дискретный марковский процесс.
Пусть нас интересует число появления некоторого случайного события на полуинтервале 
. Понятно, что такое число может быть только целым, и его значение не может принимать отрицательные значения, т.е. 
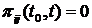при j < i.
Нетрудно убедиться в том, что вероятность появления одного события на интервале (
) есть 
. Кроме того, вероятность сохранения состояния (т.е. отсутствие события на выделенном интервале) есть 
. Отсюда вероятность появления двух или нескольких событий на этом интервале есть 
. Другими словами,
,
.
Зададим начальные условия
(2.35)
Вычислим вероятность i -го состояния в момент времени t. С этой целью построим граф состояний
Рис. 2.2. Размеченный граф состояний пуассоновского случайного процесса
и запишем уравнения Колмогорова для описания эволюции вероятностей обнаружения системы в различных доступных состояниях
(2.36)
Решая их последовательно с использованием начальных условий (2.35), находим
- при 
, - при 
.
Отсюда
. (2.37)
Аналогичное получаем при 
.
Докажем по индукции, что
. (2.38)
Напомним суть метода математической индукции.
Если для счетной последовательности утверждений 
показана справедливость первого - 
и доказано, что из предположения о справедливости 
следует справедливость 
, то все утверждения нашей последовательности верны.
Наше утверждение заключается в том, что число описанных выше событий на временном полуинтервале распределено по закону Пуассона, т.е. для любого 
вероятность появления ровно 
событий равна 
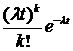. Для случаев 
и 
мы убедились в справедливости утверждения. Докажем теперь, что из справедливости 
следует 
.
Воспользуемся соответствующим уравнением Колмогорова из системы (2.36)
.
Его можно переписать в другом, эквивалентном виде
. (2.39)
Подставляя в (2.39) выражение для 
, которое, в соответствии с алгоритмом метода считается истинным, получаем
.
Полученный результат соответствует (2.38), следовательно, согласно методу математической индукции соотношение (2.38) – справедливо.
Определение 10. Марковский процесс называется циклическим, если его размеченный граф имеет вид
 |
Рис. 2.3. Размеченный граф состояний циклического процесса
Если при этом процесс однороден, то он называется однородным циклическим процессом.
