Рассмотрим случайный процесс 
такой, что:
. (3.32)
Здесь 
и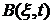 
- некоторые известные функции, обладающие рядом перечисленных ниже свойств. Сформулируем без доказательства важную теорему, описывающую свойства процесса .
Теорема 7 (Дуба). Пусть функции и 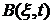измеримы и удовлетворяют локальному условию Липшица, т.е.
имеем 
.
Тогда решение (3.32) с начальным условием 
единственно с точностью до стохастической эквивалентности.
При этом:
1) непрерывна почти наверное,
2) - марковский случайный процесс,
3) если и 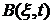непрерывны по t, то - диффузионный процесс.
Диффузионный процесс – непрерывный марковский процесс с переходной плотностью вероятности, удовлетворяющей следующим условиям: существуют функции 
и 
, называемые соответственно коэффициентами сноса и диффузии, такие, что для любого 
выполняются соотношения
Важнейшим представителем этого класса процессов является процесс броуновского движения, впервые рассмотренный как математическая модель процессов диффузии, и определивший название всего класса.
Для всякого диффузионного марковского процесса с непрерывным пространством состояний можно построить уравнение Колмогорова – Фоккера – Планка подобно тому, как это делалось для процессов с дискретным спектром.
Т.е. для переходной вероятности имеет место дифференциальное уравнение
Если известно 
, то, используя очевидное соотношение
,
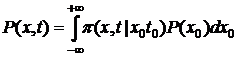можно перейти к уравнению Колмогорова – Фоккера – Планка для плотности вероятности обнаружения процесса в состоянии 
. (3.33)
Таким образом, в ряде случаев, описываемых теоремой 7, мы можем получить информацию (безусловно, не всю) о свойствах решения стохастического дифференциального уравнения (3.32), решая более простую задачу, связанную с решением дифференциального уравнения второго порядка в частных производных.
Контрольные вопросы для самопроверки
1. Перечислите свойства, которыми обладает стохастическая мера.
2. Как вводится стохастический интеграл от неслучайной функции по стохастической мере?
3. Как вводят стохастическую меру для интеграла Ито?
4. Чем стохастический интеграл Стратоновича отличается от интеграла Ито?
5. Что представляет собой стохастический дифференциал?
6. Как выглядит спектральное представление случайного процесса?
7. Что называют спектральной плотностью случайного процесса?
8. Сформулируйте содержание теоремы Винера-Хинчина.
9. Какой случайный процесс называют диффузным?
10. Сформулируйте основные результаты теоремы Дуба.
11. Запишите уравнение Колмогорова – Фоккера – Планка для переходной вероятности.
12. Проделайте переход к уравнению Колмогорова – Фоккера – Планка для плотности вероятности обнаружения процесса в заданном состоянии.
Литература
1. Боровков А.А. Теория вероятностей. - М.: Наука, 1986.
2. Булинский А.В., А.Н. Ширяев А.Н. Теория случайных процессов. - М.: Физматлит: Лаборатория базовых знаний, 2003.
3. Вентцель А.Д. Курс теории случайных процессов. - М.: Физматлит, 1975.
4. Волков И.К.,Зуев С.М., Цветкова Г.М. Теория случайных процессов. - М.: МГТУ им.Н.Э. Баумана, 1999.
5. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. -
М.: Наука, 1965.
6. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1969.
7. Карлин С. Основы теории случайных процессов. - М.: МИР, 1971.
8. Кемени Джон Дж., Снелл Дж. Лори. Конечные цепи Маркова. - М.: Наука, 1964.
9. Кокс Д.Р., Смит В.Л. Теория восстановления. - М.: Сов. радио, 1967.
10. Миллер Б.М., Панков А.Р. Теория случайных процессов в примерах и задачах. - М.: Физматлит, 2002.
11. Пугачев В.С. Теория случайных функций. - М.: Физматлит, 1962.
12. Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика. - М.: Наука, 1989.
13. Розанов Ю.А. Случайные процессы. Краткий курс. - М.: Наука, 1971.
14. Чжун Кай-лай. Однородные цепи Маркова. - М.: Мир, 1964.
