Определение 13. Скалярный случайный процесс второго порядка 
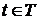называется дифференцируемым в точке 
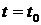, если существует такая случайная величина 
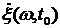, для которой
. (3.7)
При этом случайная величина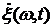 
называется его производной в этой точке.
Определение 14. Если скалярный случайный процесс второго порядка 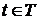является дифференцируемым в каждой точке открытого множества 
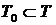, то его называют дифференцируемым на множестве 
.
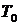Теорема 4 (необходимое и достаточное условие дифференцируемости случайного процесса). Для того, чтобы скалярный случайный процесс второго порядка 
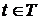был дифференцируемым в точке 
, а для случайной величины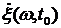 
существовало математическое ожидание и дисперсия, необходимо и достаточно, чтобы функция 
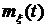была дифференцируема в этой точке и существовала вторая обобщенная смешанная производная от корреляционной функции 
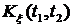при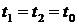 
.
Следствие 1. Для дифференцируемого на множестве T скалярного случайного процесса второго порядка 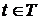с математическим ожиданием 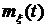и корреляционной функцией 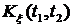определен скалярный случайный процесс 
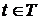, и при этом, если скалярный случайный процесс 
есть процесс второго порядка, то
1) 
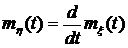; 2)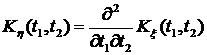 
.
Если к тому же еще и стационарный процесс, то
1) 
; 2) 
.
Пример 2. Покажем, что пуассоновский процесс стохастически непрерывен, но не дифференцируем.
Действительно, пусть = 
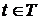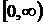- пуассоновский случайный процесс с параметром 
. Согласно определению, пуассоновского процесса 
имеет место независимость случайных величин 
и 
, которые распределены по Пуассону с параметрами 
и 
соответственно.
Если существует предел (3.7), а пространство полное, то по критерию Коши последовательность фундаментальна, если и только если она сходится.
Проверим, является ли последовательность фундаментальной, т.е. выполняется ли условие
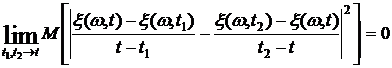. (3.8)
Возводя разность дробей в квадрат (3.8), можно переписать в виде суммы трех пределов. Учитывая, что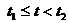 
, а пуассоновский процесс – процесс с независимыми приращениями, математическое ожидание от произведения дробей (случайных величин, пропорциональных приращениям случайного процесса на непересекающихся временных интервалах) в (3.8) «разваливается» на произведение соответствующих средних величин, которое, как нетрудно видеть, равно 
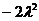. Два оставшихся члена однотипны, и могут быть вычислены достаточно просто
Учитывая, что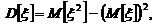 
находим
Суммируя все сказанное, приходим к следующему выражению для математического ожидания в левой части (3.8)
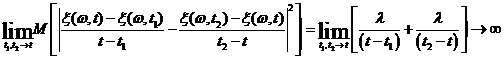
Следовательно, можно выбрать последовательность с 
и 
не являющуюся фундаментальной. Тогда, согласно критерию Коши, предела (3.8) не существует, и следовательно, процесс не дифференцируем.
