Определение 16. Скалярный случайный процесс второго порядка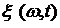 
, 
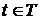=[0, l ], интегрируемый на множестве T с весом 
= 
и обладающий постоянным математическим ожиданием, называют эргодическим по отношению к математическому ожиданию 
, если справедливо
, (3.11)
т.е., если
. (3.11а)
Эргодические процессы играют большую роль в различных приложениях. Фактически соотношения (3.11), (3.11а) означают, что среднее во времени для таких процессов - 
равно среднему по ансамблю реализаций -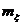 
. Т.е., для нахождения среднего достаточно продолжительного наблюдения за одной реализацией случайного процесса, что бывает удобно при различного рода экспериментальных исследованиях.
Теорема 6 (критерий интегрируемости с весом скалярного случайного процесса). Пусть 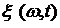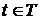=[0, l] - скалярный случайный процесс второго порядка, интегрируемый на множестве T с весом 
, где - неслучайная функция, определенная на T. Тогда
,
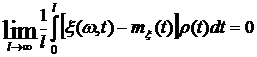если и только если существует и равен нулю предел
.
Следствие. Пусть в условии теоремы = , 
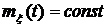, тогда необходимым и достаточным условием эргодичности случайного процесса в отношении 
является
.
Контрольные вопросы для самопроверки
1.Какие процессы называются стохастически непрерывными?
2.Должны ли стохастически непрерывные процессы иметь непрерывные реализации? Приведите пример.
3.Сформулируйте необходимое и достаточное условие стохастической непрерывности случайного процесса.
4.Какие случайные процессы называются дифференцируемыми?
5.Сформулируйте необходимое и достаточное условие дифференцируемости случайного процесса.
6.Чему равно математическое ожидание производной стационарного случайного процесса?
7.Где в доказательстве недифференцируемости пуассоновского процесса используется то, что он является процессом с независимыми приращениями?
8.Сформулируйте критерий Коши. Какая последовательность случайных величин является фундаментальной?
9.Какой случайный процесс называется интегрируемым с весом?
10. Верно ли, что оператор математического ожидания коммутирует с оператором интегрирования с весом?
11. Какие случайные процессы называются эргодическими по отношению к математическому ожиданию?
12. Сформулируйте необходимое и достаточное условие эргодичности случайного процесса.
9. Стохастическая мера и стохастический интеграл
Стохастическая мера
Определение 17. Пусть T – конечный или бесконечный отрезок действительной прямой и на его полуинтервалах вида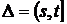 
задана случайная функция 
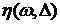со значениями в гильбертовом пространстве H случайных величин 
: 
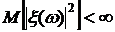. И пусть далее 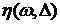обладает следующими свойствами:
1) для двух непересекающихся полуинтервалов 
и 
случайные величины 
и 
ортогональны, т.е. (, )=0 или 
;
2) 
(дизъюнктивное объединение);
3) 
.
Обобщим соотношение в 3). Рассмотрим 
(
Ǿ 
).
Отсюда 
.
Введем теперь понятие стохастического интеграла от неслучайной функции 
по стохастической мере. Мы определим этот интеграл как предел последовательности интегралов от кусочно-постоянных функций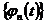 
, аппроксимирующих , показав перед этим, что такие интегралы существуют.
1) Пусть - вещественная кусочно-постоянная функция (т.е.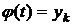 
при 
). Определим интеграл от кусочно-постоянной функции как стохастическую сумму
. (3.12)
Тогда квадрат нормы такого интеграла равен обычному риманову интегралу
(3.13)
Попутно заметим, что
.
Отметим, что все вышесказанное верно и для случая комплексной функции . Если функция комплексная, то нужно лишь использовать комплексное сопряжение.
2) Определим теперь такой же интеграл для произвольной неслучайной функции 
на T, (
интегрируема на T), допускающей аппроксимацию кусочно-непрерывными функциями 
. (3.14)
Если выполняется (3.14), то согласно критерию Коши последовательность 
фундаментальна, и имеет место предел
.
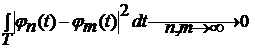Рассмотрим теперь последовательность интегралов 
. Докажем, что эта последовательность имеет предел. Для этого покажем, что это последовательность фундаментальна. Имеем
Следовательно, действительно фундаментальная последовательность. Но тогда, согласно критерию Коши, она имеет предел.
Определение 18. Стохастическим интегралом от неслучайной функции по стохастической мере 
будем называть предел
(3.15)
где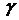 
- диаметр разбиения – 
.
