Используемые типы сходимости случайных величин позволяют ввести в пространстве всевозможных случайных величин 
вероятностную метрику 
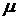, такую, что сходимость последовательности случайных величин эквивалентна сходимости 
.
Определение 7. Вероятностной метрикой в называется каждый неотрицательный функционал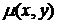 
, определенный на множестве совместных распределений 
пар случайных величин 
и обладающий следующими свойствами
1) 
;
2) 
;
3) 
.
Рассмотрим множество случайных величин 
(на некотором вероятностном пространстве 
), для которых 
. Это множество случайных величин образует гильбертово пространство H со скалярным произведением, определяемым по формуле
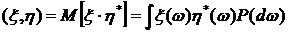. (3.1)
Введем норму случайной величины по формуле:
. (3.2)
Если взять в качестве случайной величины 
, то 
определяет расстояние между и 
в рассматриваемом гильбертовом пространстве. Кроме того, определяет так называемую среднеквадратическую метрику (с.к. метрику):
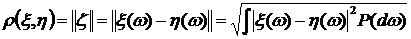. (3.3)
Определение 8. Говорят, что последовательность случайных величин 
сходится к 
в среднеквадратическом смысле, если
.
Перейдем к рассмотрению сходимости случайных процессов.
Определение 9. Пределом последовательности случайных процессов 
(если таковой существует) называется случайный процесс 
. (3.4)
Определение 10. Пределом случайного процесса 
при 
в смысле с.к. сходимости называется случайная величина
. (3.5)
Предельный переход можно понимать в смысле Гейне, т.е. рассматривать произвольную последовательность 
и вводить последовательность случайных величин 
. Тогда предел в (1.5) можно записать в виде
.
Теорема 1. Если существует предел скалярного случайного процесса при , 
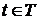, равный случайной величине , то существует предел скалярной функции 
при , и этот предел равен 
.
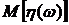Доказательство.
нужно доказать, что
.
Имеем
Здесь мы применили известное неравенство 
.
Напомним, что гильбертово пространство есть полное нормированное пространство (норма определяется скалярным произведением (3.1)), т.е. всякая фундаментальная последовательность случайных величин 
имеет в H предел.
Теорема 2 (необходимое и достаточное условие существования предела для случайного процесса). Скалярный случайный процесс , 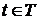имеет предел при тогда и только тогда, когд а существуют конечные пределы
Контрольные вопросы для самопроверки
1. В каком случае говорят, что случайные величины относятся к одному классу эквивалентности?
2. Какие процессы называются стохастически эквивалентными?
3. Что понимают под термином «вероятностная метрика»?
4. Как вводится среднеквадратическая метрика?
5. Что есть предел последовательности случайных процессов?
6. Что понимают под термином «предел случайного процесса»?
7. Каковы необходимые и достаточные условия существования предела случайного процесса?
