В работе предложена модель прогнозирования состояния остатков на бухгалтерских счетах предприятия на основе математического аппарата марковских процессов. Рассмотрены этапы построения модели для заданного плана счетов и описываются основные приближения.
Ключевые слова: бухгалтерский план счетов, марковские процессы, математическое моделирование.
Введение
В современном мире многие предприятия поставлены в условии я самостоятельного выбора стратегии и тактики своего развития. Важными элементами успешной коммерческой деятельности являются мероприятия по анализу и прогнозированию финансового состояния компании. Первоочередным объектом анализа выступают оборотно-сальдовые ведомости, составленные на основе состояния бухгалтерских счетов. Однако, на основе исключительно бухгалтерского учета невозможно провести постановку задачи прогнозирования. В этом случае наиболее перспективным видится использование
инструментов математического моделирования, которые играют значительную роль в современной экономике и финансах, что подчеркивает актуальность работ, посвященных данной тематике.Из описанного выше сформулируем цель работы - разработать математическую модель прогнозирования состояния остатков бухгалтерских счетов для проведения исследований по оценке стратегий управления и развития предприятия.
Описание модели
Любая финансовая деятельность компании отражается на бухгалтерских счетах, правила ведения которых регламентируется соответствующими нормативными документами [1].
Состояние конкретного счета предприятия определяется остатком денежных средств на на фиксированный момент времени. Любое финансовое действие отражается в виде изменения остатков на двух или более счетах. При этом используется бухгалтерское правило двойной записи, отражающее взаимосвязанные изменения счетов. В случае, когда для двух корреспондирующих счетов один является активным, а другой - пассивным, соответствующая операция приводит к уменьшению остатков на пассивном счете и увеличению на активном на равную денежную сумму. Таким образом, любая денежная единица может перечисляться с одного счета на другой. Это позволяет провести аналогию между счетами предприятия и состояниями некоторого процесса, который описывает движение конкретной денежной единицы. Наличие множества денежных единиц и операций, затрагивающих различные счета, данный процесс можно смоделировать в терминах теории случайных процессов.
Важным шагов в построении модели является гипотеза о марковости [2, 3] рассматриваемого процесса, которую можно не строго обосновать следующими рассуждениями. Попадая на конкретный счет, денежные средства могут быть перечислены на любой из корреспондурующих счетов в не зависимости от прошлых состояний, в которых они находились. Таким образом, для дальнейшего построения модели необходимо формализовать основные элементы бухгалтерского плана счетов в терминах марковских цепей с непрерывным временем. Рассмотрение непрерывного по времени процесса видится более адекватным для ситуации со множеством финансовых операций на промежутке времени и представляется более интересным для дальнейших исследований. Рассмотрим марковский случайный процесс, в котором количество состояний определяется набором счетов из конкретного плана счетов предприятия. При этом для упрощения не будем рассматривать детализацию до уровня субсчетов. Для каждого состояния i =1, n определим вероятность нахождения Pi процесса в данном состоянии как долю денежных находящихся на остатках счета, соответствующего i -у состояния. При построении графа данного процесса корреспондирующие счета следует соединить ребрами по следующему правилу. Проводка, уменьшающая остатки на счете i и увеличивающая остатки на счете j изображается ребром (i, j). Пример подобного построения для элементов общего плана счетов приведён на рис 1.Отметим, что подобный подход работает только для проводок, которые затрагивают разные типы счетов (один из счетов активный, другой пассивный). Случай, когда и счет дебета и счет кредита имеют один и тот же тип требует отдельного изучения и в данной работе не рассматривается. Важной характеристикой марковской цепи с непрерывным временем является матрица плотностей вероятностей переходов Λ. Элементы данной матрицы λ ij определяются следующим соотношением
λ ij =limΔ t →0 Pij Δ t , (1)
Где Pij - условная вероятность перехода системы из j -ого в i -ое состояние.
В соотношении (1) предполагается, что условная вероятность не зависит от времени, что позволяет рассматривать процесс как стационарный. Подобное ограничение не позволяет получать адекватные результаты в условиях существенного изменения характера финансовых операций и не может быть использовано при решении вопросов оценки стратегии развития. Поэтому в работе предлагается рассмотреть случай нестационарного марковского процесса, при котором плотность вероятности переходов зависит от времени λ ij =λ ij (t).
Для определения плотностей вероятностей переходов предлагается следующую гипотезу.Будем считать, что, для данной модели, значение λ ij можно представить как интенсивность денежного потока между соответствующими счетами за некоторый период времени T. Тогда, вместо выражения (1) будем использовать следующую оценку
λ ij =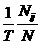 
, (2)
Где Nij - количество проводок с j -ого счета на i -й счет за период времени T, и N - общее количество проводок за выбранный период.
Следующий шаг при построении модели заключается в записи уравнений Колмогорова, описывающих эволюцию вероятностей нахождения системы в соответствующих состояниях[3]
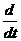Pi (t)=Σ j λ ij Pj (t)-Σ k λ ki Pk (t), i =1, …, n -1. (3)
В правой части (3) первая и вторая суммы берутся по всем входящим в i -ую вершину ребрам и исходящим из i -ой вершины ребрам соответственно.Уравнение (3) следует дополнить условием нормировки
Pn (t)=1-Σ iPi (t), i =1, …, n -1. . (4)
В качестве начальных условий для системы уравнений (3), (4) следует использовать начальное сальдо по рассматриваемым начальное сальдо по рассматриваемым счетам.
Результаты интегрирование полученной системы позволят построить прогноз состояний счетов компании в зависимости от выбранной стратегии развития, управление которой может быть осуществлено путём увеличения объемов выбранных проводок. Интересным элементом исследований данной модели видится постановка задачи теории управления, где в качестве целевой функции может выступать, например, увеличение средств на основном счету компании, а в качестве управления изменение количество финансовых проводок.
Заключение
В работе предложена модель прогнозирования состояния бухгалтерских счетов предприятия на основе математического аппарата марковских процессов. Рассмотрены вопросы построения графа переходов состояния марковского процесса на основе бухгалтерского плана счетов и оценки плотностей вероятностей переходов между состояниями путем анализа финансовых проводок за выбранный период. Обсуждены вопросы построения прогнозов состояния остатков на счетах и оценки стратегий развития на основе управления количеством финансовых операций.
Литература
1. Приказ Минфина России от 02.07.2010 № 66н «О формах бухгалтерской отчетности организаций»
2. Гихман И.И., Скороход А.В. Теория случайных процессов Т. 1. - М.: Наука, 1971
3. Дынкин Е.Б. Основания теории марковских процессов. - М: Физматгиз, 1959
Случайные процессы, основные понятия, их классификация, теорема Маркова о транзитивных цепях, эргодическая теорема, уравнение Чепмена-Колмогорова для дискретных и непрерывных цепей.
Цепь Маркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего).
