Рассмотрим случайный процесс 
, который принимает только конечное число значений 
. В отличие от марковской цепи, переходы между состояниями в этом процессе могут происходить не только в выбранный дискретный момент, но и в произвольный момент времени.
Введем вероятность перехода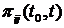 
. (2.16)
Заметим, что
, (2.17)
. (2.18)
При этом справедливо уравнение Маркова
, (2.19)
которое называют также уравнением Колмогорова – Чепмана.
Основная задача в теории марковских процессов состоит в вычислении:
1. Вероятности перехода 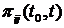при 
.
2. Вероятностей различных состояний 
для 
по известным начальным состояниям системы и локальным характеристикам вероятностей перехода.
Определение 7. Пусть S – некая система с дискретным пространством состояний. Под плотностью вероятностей (или интенсивностью) перехода из состояния 
в состояние 
при 
в момент времени t понимают величину 
, равную
. (2.20)
Таким образом, для малых 
можно записать
.
Для дискретных марковских процессов для малых 
вероятности переходов могут быть записаны в виде
, (2.21а)
. (2.21б)
Отсюда следует, что при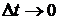 
система, первоначально находившаяся в состоянии i, почти наверное останется в этом состоянии, а вероятность перехода в другое состояние будет пропорциональна .
Из условия нормировки можно записать:
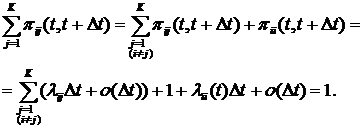(2.22)
Отсюда следует, что
. (2.23)
Подставив (2.21а), (2.21б) в (2.19), находим
.
Отсюда
.
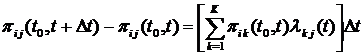Деля последнее уравнение на и переходя к пределу при 
, получим систему прямых уравнений Колмогорова
. (2.24)
Система уравнений (2.24) при начальных условиях 
- (2.18) дает зависимость вероятности перехода из i в j как функцию времени.
Можно показать, что если число состояний системы конечно (в нашем случае К), то для любых непрерывных функций 
, удовлетворяющих условию (2.23), система уравнений (2.24) с начальными условиями (2.18) имеет единственное неотрицательное решение, которое определяет дискретный марковский процесс.
В уравнении (2.24) фигурирует частная производная, т.к. 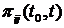- это функция двух переменных. Можно менять начальный момент времени 
, а можно конечный t. Меняя , получим по аналогии с (2.24) систему обратных уравнений Колмогорова
. (2.25)
Системы уравнения (2.24), (2.25) записываются соответственно в матричном виде
(2.26)
, (2.27)
где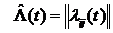 
.
Умножая обе части (2.24) на 
, а затем суммируя по i и, учитывая
,
получим
, (2.28)
Так как. (2.23)
,
то (2.28) можно переписать в следующем виде
. (2.29)
В записанном виде уравнению Колмогорова можно придать некий физический смысл. Для этого введем понятие «потока вероятности»
– поток вероятности из i -го состояния в j -е.
Тогда скорость изменения вероятности обнаружения системы в j -м состоянии равна сумме потоков вероятностей, переводящих систему в это состояние, минус сумма потоков вероятностей, выводящих систему из этого состояния.
Определение 8. Скалярный марковский процесс с дискретным пространством состояний называется однородным, если 
зависит только от разности времен, от величины 
.
Предложение 1. Для однородного марковского процесса с дискретным пространством состояний интенсивности переходов не зависят от времени:
.
Действительно,
.
Так как дляоднородного марковского процесса 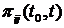зависит только от , то имеют место соотношения
, (2.30)
. (2.31)
Теорема 2. Для однородного марковского процесса с дискретным пространством состояний имеем
. (2.32)
Кроме того,
, (2.33)
т.е., если процесс однородный, то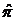 
и 
коммутируют. При этом решение (2.33) имеет вид
, (2.34)
где 
– единичная матрица, 
.
Доказательство. (2.32) есть матричная запись (2.30) и (2.31). (2.33) следует из (2.32),(2.26), (2.27). Ясно теперь, что (2.34) есть решение (2.33) с начальным условием .
Определение 9. Множество состояний системы называется эргодическим, если из любого состояния можно перейти в состояние .
Можно показать, что для эргодического процесса, по истечении достаточно большого промежутка времени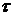 
, вероятность того, что система будет находиться в состоянии , не зависит от того, в каком состоянии 
система находилась в начальный момент времени.
