Цепи Маркова
Определение цепи Маркова
Рассмотрим некую физическую систему, которая может находиться в одном из K состояний 
. Пусть далее вследствие вмешательства случая система шаг за шагом в заданные моменты времени 
может скачкообразно случайным образом менять свое состояние 
., где 
– какое-либо значение из .
Полное вероятностное описание поведения системы за n шагов задается совместными конечномерными вероятностями 
.
Таких вероятностей много, столько, сколько различных путей может быть проложено в системе. Будем полагать, что процесс переходов между состояниями обладает марковским свойством. Тогда вероятность каждой реализации может быть записана в следующем виде
(2.1)
Напомним, что процесс называется марковским, если
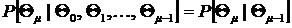. (2.2)
Определение 1. Случайная последовательность 
(т.е.,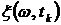 
– случайный процесс в дискретном времени) со значениями в дискретном пространстве состояний называется цепью Маркова, если справедливо соотношение (1.2).
Определение 2. Условную вероятность 
, дающую вероятность того, что на n –м шаге состояние системы примет значение 
при условии, что на (n-1) -ом шаге система была в состоянии 
принято называть переходной вероятностью или вероятностью перехода.
Аналогично –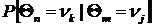 
, можно записать вероятность (n- m) -шагового перехода (здесь n> m), то есть условную вероятность того, что система, находящаяся на m -ом шаге в состоянии , на n –ом шаге окажется в состоянии .
Уравнение Маркова
Основная задача для марковских цепей.
Пусть известно начальное состояние системы и указан вероятностный закон смены состояний (указаны все соответствующие вероятности одношаговых переходов). Тогда основная задача для марковских цепей заключается в следующем:
каким образом можно найти вероятность состояния системы в некоторый момент времени 
(в частности, при 
)?
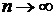Для удобства введем следующие обозначения для условной и безусловной вероятностей
(2.3)
Т.к. система на n –м шаге в каком-нибудь состоянии обязательно будет находиться, то полное пространство исходов эксперимента полно, и
(2.4)
Далее, если система находится в i -м состоянии, то она либо останется в нем, либо перейдет в любое другое состояние. Третьего не дано. Поэтому сумма вероятностей многошагового перехода по всем возможным конечным состояниям (исходам) должна давать единицу:
(2.5)
Нетрудно убедиться в том, что согласно формуле полной вероятности, имеет место следующая связь
(2.6)
Рассмотрим теперь подробнее структуру многошагового перехода. Переходя из j–го состояния на 
м шаге в 
е состояние на n –м шаге, система обязательно побывает в одном из 
состояний на m -м шаге (рис.-2.1)
Рис. 2.1. Схема изменений состояния системы с о по n –й шаг
Совокупность переходов, указанных на рисунке пунктиром, представляют собой множество несовместных событий. Поэтому вероятности реализаций таких переходов складываются. Вместе с тем, каждый отдельно взятый переход представим в виде последовательности двух переходов 
и 
. В силу марковости процесса, реализация перехода из какого-либо 
состояния на m -м шаге в е состояние на n –м шаге не зависит от того, как система попала в 
состояние. Поэтому вероятность такой реализации равна произведению вероятностей соответствующих переходов – 
. Полная же вероятность перехода в этом случае равна
(2.7)
Определение 3. Соотношение (2.7) для дискретных цепей Маркова с конечным числом состояний принято называть уравнением Маркова.
Отметим, что уравнение Маркова – это частный случай уравнения Колмогорова-Чепмена для случая бесконечного числа промежуточных состояний.
Введем квадратную матрицу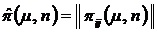 
и матрицу-строку 
, тогда (2.6) и (2.7) можно записать в матричном виде
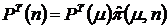, (2.6а)
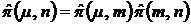. (2.7а)
Определение 4. Квадратная матрица 
с неотрицательными элементами, удовлетворяющая условию 
, называется стохастической.
Записанное матричное уравнение (2.6а) можно транспонировать
.
Используя уравнение Маркова в виде (2.7а), матрицу 
можно представить в виде произведения
(2.8)
Полагая в (2.8) 
, находим
. (2.9)
Из (2.9) следует, что полное вероятностное описание цепи Маркова достигается заданием 
- вероятности начального состояния и последовательности матриц вероятностей одношаговых переходов – 
.
Определение 5. Марковская цепь, для которой матрица вероятностей одношаговых переходов не зависит от номера шага, называется однородной.
Если матрица 
удовлетворяет условию однородности, то
(2.10)
Матрицу 
будем обозначать через 
. Тогда соотношение (2.7а) можно переписать в виде
. (2.11)
Для одношагового перехода положим
.
Нетрудно видеть, что
Для однородной цепи Маркова матрица вероятностей перехода за n шагов равна n -й степени матрицы одношагового перехода. Отсюда
. (2.12)
Определение 6. Однородная цепь Маркова, для которой вероятности 
не зависят от n, называется стационарной. В противном случае цепь называется нестационарной.
Для стационарной цепи имеют место соотношения
, (2.13)
, (2.14)
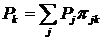. (2.15)
Одна из важнейших задач теории марковских цепей состоит в исследовании вопроса, существует ли для данной марковской цепи некая стационарная цепь, к которой сходится исходная цепь. Другими словами, существует ли предел 
? Если такой предел существует, то марковская цепь сходится к стационарной.
Теорема 1. Если для цепи Маркова с конечным числом состояний выполняется условие 
, то существуют предельные (финальные) вероятности 
, причем не зависит от начального распределения 
.
Очевидно, что находится из системы К уравнений
и условия нормировки 
.
Замечание 1. Однородную цепь Маркова удобно представлять в виде ориентированного графа, вершины которого – возможные состояния цепи, а дуги выписаны переходными вероятностями.
Контрольные вопросы для самопроверки
1.Какие случайные процессы называются цепями Маркова?
2.В чем суть основной задачи для марковских цепей?
3.Почему одно из соотношений (2.5) можно назвать «условием нормировки»?
4.Где в уравнении Маркова «зашито» условие марковости?
5.Какие матрицы называются стохастическими?
6.Каково требование однородности для цепи Маркова?
7.Является ли стационарная марковская цепь однородной?
8.Что такое предельные вероятности?
9. Каким условиям должна удовлетворять марковская цепь для того, чтобы для нее существовали финальные вероятности?
