Случайный процесс, эволюция которого после любого фиксированного момента времени t и до момента времени t является условно независимой при известном состоянии процесса в момент времени t (в настоящем), называется марковским случайным процессом, а свойство условной независимости «будущего» от «прошлого» при заданном «настоящем» называется марковским свойством или свойством марковости.
Определение 36. Пусть 
– случайный процесс, конечномерные функции плотности вероятности которого 
заданы для всех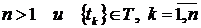 
: 
. Если при этом условная функция плотности вероятности
, (1.26)
где 
– состояние в данный момент; 
– состояние в будущем; 
– прошлые состояния, то случайный процесс называется марковским процессом.
Пример 4. Пример марковского процесса, используемого в модели расчета риска столкновений воздушных судов.
Рассмотрим полет воздушного судна, с которым может произойти катастрофа, которую мы рассматриваем здесь как мгновенное событие. Введем некоторую случайную функцию 
, описывающую состояние воздушного судна
Покажем, что – марковский случайный процесс.
Если в момент 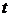времени 
, то прошлое – нормальный полет, не дает никакой информации о том, произойдет катастрофа в будущем или нет. Прошлое не информативно для будущего. Если же в момент времени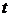 
, то есть на текущий момент факт катастрофы имеет место, то для описания состояния в будущем неважна информация из прошлого о том, когда эта катастрофа произошла.
Определение 37. Пусть на вероятностном пространстве 
задан случайный процесс 
со значениями в измеримом пространстве, 
– пространство состояний. Для 
введем 
-алгебру прошлого 
(все реализации случайного процесса 
, где 
) и будущего 
(определена на реализациях после момента времени t). Случайный процесс называется марковским процессом, если 
и любого события А из -алгебры прошлого 
и В из -алгебры будущего 
имеет место марковское свойство:
.
При таком определении прошлое и будущее симметричны, т.е. переходя в обратное время 
при переходе к отраженному процессу 
, марковское свойство сохраняется.
Контрольные вопросы для самопроверки
1. Каким условиям удовлетворяют случайные процессы, стационарные в узком смысле?
2. Можно ли сказать, что процесс, стационарный в узком смысле, стационарен и в широком смысле?
3. Чему равна производная от математического ожидания стационарного в узком смысле процесса?
4. Какой случайный процесс называется нормальным?
5. Что такое характеристическая функция?
6. Приведите пример двумерного гауссового процесса.
7. Какой процесс называется процессом с независимыми приращениями?
8. В чем отличие независимых и ортогональных приращений?
