Определение 25. Корреляционной функцией (автокорреляционной функцией, функцией корреляции ) комплексного случайного процесса или комплексной случайной функции  называют неслучайную функцию
называют неслучайную функцию  , определяемую равенством
, определяемую равенством
 , (1.16)
, (1.16)
где 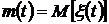 ,
, 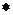 – комплексное сопряжение.
– комплексное сопряжение.
Предложение 3. Корреляционная функция обладает следующими свойствами:
1)  (неотрицательность);
(неотрицательность);
2) 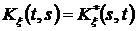 (эрмитовость);
(эрмитовость);
3)  ;
;
4)  (неотрицательная определенность) для любых
(неотрицательная определенность) для любых  и любых комплексных чисел
и любых комплексных чисел 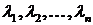 .
.
Доказательство. 1)  . 2) следует непосредственно из определения
. 2) следует непосредственно из определения  .
.
Доказательство остальных свойств аналогично их доказательству для корреляционной матрицы семейства случайных величин.
Замечание 4. Для вещественной случайной функциикорреляционная функция обладает следующими свойствами:
1)  (неотрицательность);
(неотрицательность);
2)  (симметричность);
(симметричность);
3)  ;
;
4)  (неотрицательная определенность) для любых
(неотрицательная определенность) для любых  и любых действительных чисел
и любых действительных чисел 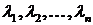 .
.
Замечание 5. Положим
 .
.
Тогда корреляционная функция записывается в виде
 .
.
Определение 26. Нормированная корреляционная функция случайного процесса ξ(t) (вещественного или комплексного) определяется формулой
 .
.
Предложение 4. Нормированная корреляционная функция обладает следующими свойствами:
1)  ;
;
2)  ;
;
3)  ;
;
Доказательство следует непосредственно из предложения 3.
Принципиальное отличие корреляционной функции 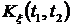 некоторого случайного процесса от математического ожидания
некоторого случайного процесса от математического ожидания 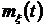 и дисперсии
и дисперсии  того же случайного процесса заключается в том, что при нахождении корреляционной функции берутся два сечения случайного процесса, а не одно, как в случае
того же случайного процесса заключается в том, что при нахождении корреляционной функции берутся два сечения случайного процесса, а не одно, как в случае 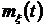 и
и  .
.
Для нахождения корреляционной функции необходимо использовать двумерную функцию распределения случайного процесса  . При этом если существует двумерная плотность, то корреляционная функция имеет вид
. При этом если существует двумерная плотность, то корреляционная функция имеет вид
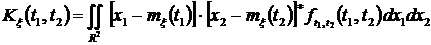 , (1.17)
, (1.17)
где  в точках, где
в точках, где  дважды непрерывно дифференцируема.
дважды непрерывно дифференцируема.
Заметим, что при интегрировании (3.6) часть информации теряется и корреляционная функция содержит меньше информации о случайном процессе, чем двумерная функция распределения.
Если 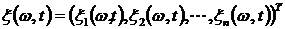 многомерный случайный процесс такой, что
многомерный случайный процесс такой, что  для
для  , то его корреляционной функцией называют матричнозначную корреляционную функцию
, то его корреляционной функцией называют матричнозначную корреляционную функцию
 , (1.18)
, (1.18)
где  .
.
Иногда вводят также нормированную взаимную корреляционную функцию случайных процессов 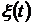 ,
, 
 . (1.19)
. (1.19)
Контрольные вопросы для самопроверки
1. Чем математическое ожидание случайного процесса отличается от математического ожидания случайной величины?
2. Как определяется математическое ожидание непрерывного случайного процесса?
3. Что понимают под дисперсией случайного процесса?
4. Что можно сказать о процессе, если его дисперсия равна нулю, а математическое ожидание – периодическая функция времени?
5. Что называют центрированным случайным процессом?
6. Что характеризует стандартное отклонение случайного процесса?
7. Какими свойствами обладает корреляционная функция?
8. Какова размерность функции распределения случайного процесса, которую необходимо использовать для вычисления корреляционной функции?
9. Каково максимальное значение нормированной корреляционной функции?
10. В каких случаях пользуются термином взаимная корреляционная функция?






