Стохастически эквивалентные случайные процессы

Стохастическая эквивалентность – отношение эквивалентности между случайными величинами, различающимися на множестве нулевой вероятности (на множестве вероятностной меры нуль).

Определение 17. Случайные величины 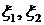, заданные на одном вероятностном пространстве , называются стохастически эквивалентными, если:

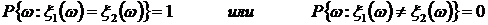    (1.7).

В большинстве задач теории вероятности работают не с самими случайными величинами, а с классами эквивалентных случайных величин.

Определение 18. Случайные процессы 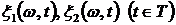, определенные на одном вероятностном пространстве, называются стохастически эквивалентными, если  имеет место стохастическая эквивалентность между соответствующими случайными величинами, т.е.

.

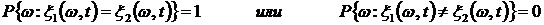Замечание 2. По отношению к случайным процессам , у которых совпадают соответствующие конечномерные распределения, применяют также термин «стохастическая эквивалентность в широком смысле». Заметим, что если случайные процессы эквивалентны, то они эквивалентны в широком смысле.

Элементарные случайные процессы

Определение 19. Элементарной случайной функцией будем называть композицию или суперпозицию элементарных функций, аргументами которых является параметр  и случайная величина , не зависящая от времени.

Пример 1

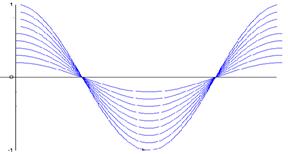
Примером простейшей элементарной случайной функцией может служить процесс вида 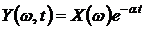, где  – равномерно распределенная на отрезке 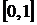случайная величина, а  и 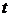 – положительные параметры. Семейство реализации  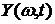показано на рис. 2. При любом фиксированном 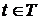, например 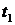, можно ассоциировать величину  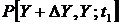с долей траекторий (от полного их числа, изображенного на рисунке), пересекающих прямую  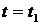на интервале .

 

 

 

 

 

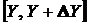Рис. 1.2. Семейство реализаций элементарной случайной функции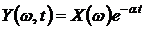

Пример 2

Рассмотрим теперь другую элементарную случайную функцию. Пусть 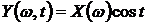, где  – равномерно распределенная на отрезке 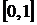 случайная величина. Семейство реализации  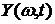для нее показано на рис.3

Рис. 1.3. Семейство реализаций элементарной случайной функции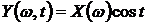

Контрольные вопросы для самопроверки

1. Как определяется случайная функция?

2. Чем случайный процесс отличается от случайной функции?

3. Что называют реализацией случайного процесса?

4. Как получить сечение случайного процесса?

5. Что называют пространством состояний случайного процесса?

6. Назовите основные классы случайных процессов, если в основу классификации положены характеристики пространства состояний.

7. Что называют одномерной функцией распределения случайного процесса?

8. Почему невозможно полностью задать случайный процесс, используя его сечения?

9. Какие процессы называются стохастически эквивалентными?

10.  О каких множествах говорят, что они имеют вероятностную меру нуль?

11.  Что означает стохастическая эквивалентность в широком смысле?

12.  Что называют элементарным случайным процессом?

13.  Приведите три примера элементарных случайных процесса.