Определение 3. Пусть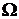 
– непустое множество. Непустое семейство 
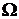подмножеств из называется 
- алгеброй, если выполняются следующие два условия:
1. Если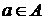 
, то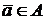 
.
2. Если 
(
), то 
.
Предложение 2. Пусть – - алгебра. Тогда
а) 
, 
;
б) если (), то 
;
в) - алгебра является алгеброй;
г) для конечного множества 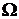любая алгебра является и - алгеброй;
д) 
- алгебра замкнута относительно любого числа любых теоретико-множественных операций.
Доказательство. Мы остановимся на доказательстве в). Остальные утверждения доказываются аналогично предложению 1.
Полагая в условии 2 определения 3 
при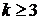 
, находим 
для всех 
.
Определение 4. Пару 
, состоящую из непустого множества 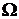и -алгебры , называют измеримым пространством.
Определение 5. Вероятностью (или вероятностной мерой) на измеримом пространстве 
называют числовую функцию 
, определенную на -алгебре , удовлетворяющую следующим трем условиям:
1. 
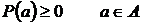(неотрицательность 
).
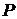2. 
(нормированность ).
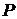3. Для любых попарно непересекающихся событий 
имеет место
(счетная аддитивность ).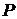
Покажем, что 
. Действительно, 
. Применяя аксиому счетной аддитивности, находим
,
следовательно .
Определение 6. Множество 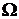, на котором задана -алгебра событий, называется пространством элементарных событий. При этом элементы -алгебры называются событиями.
Определение 7. Достоверным событием называется событие, совпадающее с самим множеством 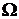. Невозможным событием называется пустое множество.
Определение 8. Вероятностным пространством называют упорядоченную тройку векторов 
, образованную из непустого множества 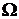заданной на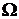 -алгеброй и определенной на -алгебре вероятностной мерой .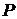
Случайные величины
Определение 9. Отображение 
измеримого пространства в измеримое пространство 
называют измеримым, если 
его прообраз 
.
Измеримое отображение 
преобразует вероятностную меру Р на в вероятностную меру 
на , определяемую равенством 
, превращая измеримое пространство в вероятностное пространство 
.
При переходе в новое вероятностное пространство описание случайного эксперимента может быть более удобным, что в свою очередь позволяет перейти от случайных событий к случайным величинам, случайным числам, случайным векторам:
1. В качестве множества 
рассмотрим множество вещественных чисел.
2. В качестве В выберем -алгебру, порожденную всеми открытыми, замкнутыми, полуоткрытыми промежутками числовой оси:
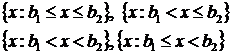
Такие множества называются борелевскими множествами, а соответствующая -алгебра называется борелевской - алгеброй.
Определение 10. Случайной величиной на вероятностном пространстве называют всякую измеримую функцию 
со значениями в R, определенную на .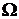
Определение 11. Распределением произвольной случайной величины называется мера 
(
, заданная на -алгебре борелевских множеств на R.
Напомним, что функция распределения случайной величины определяется как
. (1.1)
Определение 12. Случайную величину, принимающую не более, чем счетное множество значений, называют дискретной случайной величиной.
Определение 13. Непрерывной случайной величиной называют случайную величину, функция распределения которой представляется в виде
. (1.2)
называется функцией плотности распределения или просто плотностью.
Определение 14. Математическим ожиданием (если существует) случайной величины 
называется число
, (1.3)
где 
– вероятностная мера для элемента 
пространства элементарных событий .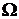
Если – непрерывная случайная величина, то
. (1.4)
Если – дискретная случайная величина, принимающая значения 
, то
, (1.5)
где 
.
Контрольные вопросы для самопроверки
1.Каким условиям должны удовлетворять элементарные исходы испытаний?
2.Что называют пространством элементарных событий?
3.Перечислите свойства событий образующих алгебру?
4.В чем основное отличие 
алгебры событий от алгебры?
5.Какое пространство называется измеримым?
6.Как вероятностная мера вводится в аксиоматике Колмогорова?
7.Что называют вероятностным пространством?
8.Дайте определение измеримого отображения.
9.Как вводится борелевская алгебра?
10. Определите понятие случайной величины с помощью измеримого отображения.
11. Какие случайные величины называются дискретными, а какие – непрерывными?
12. Запишите явный вид оператора математического ожидания для дискретных и непрерывных случайных величин.
