Теория случайных процессов
Учебное пособие
Кафедра математического анализа
ДЛЯ СТУДЕНТОВ IV КУРСА
СПЕЦИАЛЬНОСТИ ДНЕВНОГО ОБУЧЕНИЯ
2011
517.8
В учебном пособии излагаются основы теории случайных процессов. Рассматриваются основные классы случайных процессов, их основные свойства. Достаточно подробно анализируются случайные процессы в дискретном пространстве состояний с дискретным и непрерывным времени. Значительное внимание уделяется таким вопросам стохастического анализа, как стохастическая эквивалентность, непрерывность, дифференцируемость и интегрируемость случайных процессов.
Данное учебное пособие издается в соответствии с рабочей программой учебной дисциплины «Теория случайных процессов» по Учебному плану для студентов III курса специальности дневного обучения.
Оглавление
Глава 1 Основные понятия и определения
§1. Основные понятия теории вероятностей…
1.1. Вероятностное пространство……………………………
1.2. Аксиоматическое определение вероятности (аксиоматика Колмогорова)
1.3. Случайные величины…………………………………….
Контрольные вопросы для самопроверки
2. Случайные функции и случайные процессы…………………
2.1. Определение случайного процесса………………………
2.2. Предварительная классификация случайных процессов..
2.3. Способы задания, описания случайных процессов……..
2.4. Стохастически эквивалентные случайные процессы…..
2.5. Элементарные случайные процессы…………………….
Контрольные вопросы для самопроверки
3. Числовые характеристики случайного процесса…………….
3.1. Математическое ожидание и дисперсия случайного процесса
3.2. Корреляционная функция случайного процесса………..
Контрольные вопросы для самопроверки……………….
4. Основные классы случайных процессов………………………
4.1. Стационарные случайные процессы……………………
4.2. Гауссовы (нормальные) случайные процессы………….
4.3. Процессы с независимыми приращениями…………….
4.4. Марковские случайные процессы………………………
Контрольные вопросы для самопроверки
Глава 2. Марковские процессы с дискретным пространством состояний.
5. Цепи Маркова…………………………………………………...
5.1. Определение цепи Маркова………………………………
5.2. Уравнение Маркова………………………………………
Контрольные вопросы для самопроверки
6. Дискретные марковские процессы……………………………
6.1. Уравнение Колмогорова для дискретных марковских процессов
6.2. Типовые дискретные марковские процессы…………….
Контрольные вопросы для самопроверки
Глава 3 Элементы стохастического анализа ………………………………
7. Сходимость случайных процессов…………………………….
7.1. Сходимость случайных величин. Виды сходимости…..
7.2. Среднеквадратическая сходимость из группы А………..
Контрольные вопросы для самопроверки
8. Непрерывность, дифференцируемость и интегрируемость случайных процессов
8.1 Стохастическая непрерывность случайных процессов…
8.2. Дифференцируемость случайного процесса……………
8.3. Интегрируемость случайного процесса…………………
8.4. Эргодичность случайных процессов……………………..
Контрольные вопросы для самопроверки
9. Стохастическая мера и стохастический интеграл……………
9.1. Стохастическая мера……………………………………..
9.2. Стохастический интеграл Ито и стохастический дифференциал
9.3. Спектральное представление стационарных случайных процессов
9.4. Стохастические дифференциальные уравнения и уравнения Колмогорова для марковских процессов с непрерывным пространством состояний………………………
Контрольные вопросы для самопроверки………………
Литература………………………………………………………………………
Глава 1 Основные понятия и определения
Основные понятия теории вероятностей
Вероятностное пространство
Общая теоретико-вероятностная схема основана на предположении о том, что для некоторого повторяемого испытания (эксперимента), результат которого заранее предсказан быть не может, имеется совокупность элементарных исходов или элементарных событий (элементарный исход принято обозначать символом 
), и при этом должны выполняться следующие два условия:
1.Каждое испытание заканчивается одним из исходов помеченного набора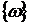 
.
2.Все исходы должны быть взаимоисключающими, т.е. конкретное испытание не должно завершаться двумя или несколькими исходами.
Определение 1. Множество элементарных исходов называется пространством элементарных событий и обозначается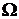 
. Событием называется любое подмножество множества элементарных исходов.
Замечание 1. Приведенное вышеопределение события пригодно для конечного или счетного пространства элементарных исходов. Оно уточняется в п.1.2.
Определение 2. Алгеброй множеств 
называется класс подмножеств непустого множества 
, удовлетворяющий следующим двум условиям:
1. Если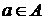 
, то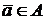 
. Здесь 
– дополнительное событие.
2. Если 
и 
, то 
.
Предложение 1. Пусть – алгебра. Тогда
а) 
;
б) 
;
в) если и , то 
;
г) если и , то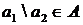 
;
д) если 
и , то 
(симметричная разность);
е) Алгебра замкнута относительно конечного числа теоретико-множественных операций.
Доказательство
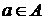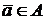а) Если , то и 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) здесь достаточно выразить все операции через 
, а затем применить индукцию.
