Комментарии к примеру анализа сопряженности.

      1. При проведении анкетирования оказались возможны четыре типа ответов: АВ,  
А , 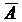В, 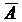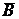. В четырех основных клетках таблицы 1 представлены численности каждой из четырех возможных групп. Например, a =36 – это численность тех, кто спортом занимался, но  к концу рабочего дня чувствовал утомление.

  2. Оба коэффициента, Q и Ф, могут принимать значения в диапазоне от ­1 до +1, и равны 0, если признаки А и В статистически независимы. Свойства коэффициентов Q и Ф легче обсуждать, имея в поле зрения формулы (1) и (2) для их вычисления.

      3. При полной положительной связанности коэффициент Q принимает значение Q=+1. Как видно из формулы (1), так было бы, если   b =0 или c =0. Это соответствовало бы тому, что среди анкетированных не оказалось субъектов типа А  или 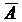В. Значению Q=−1 соответствует полная отрицательная сопряженность. Q=−1, если а =0 или d=0, т.е. если среди опрошенных не оказалось никого из АВ или.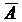

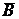
    4. Коэффициент Ф=+1, если одновременно b=0 и c=0, т. е при отсутствии субъектов А 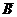 и 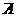В, и при наличии только АВ и .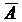

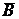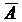
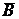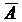. Другая крайность: Ф=−1 при а=0 и d=0, если не оказалось бы никого из АВ и , и мир состоял бы лишь из   А  и В.

   5. Числовые значения коэффициентов Q и Ф для одних и тех же данных могут существенно отличаться друг от друга, поскольку они отражают различные аспекты связей, представленных таблицей. Так, в нашем примере, Q=−0.779, в то время, как Ф=−0.423. Оба коэффициента отрицательные. Отрицательная сопряженность означает, что наличие свойства А (занятия спортом) чаще всего связано, с   (т.е. с отсутствием утомляемости). При этом коэффициент Ф по модулю меньше, чем Q, что свидетельствует о том, что в связи нет полной взаимности. Действительно, не испытывают утомления в конце работы 40 опрошенных, из них физкультурников - 28 (т.е. 70%). В то же время всего занимающихся спортом – 64 опрошенных, и из них не утомляются к концу работы – 28 (т.е. 43.8%). Как видим, ситуация не вполне симметричная: процент «неутомимых» среди «физкультурников» оказался существенно больше, чем процент «физкультурников среди «неутомимых».

    6. Результаты анализа, проведенного в нашем примере, отнюдь не тривиальны, если учесть, что среди двухсот опрошенных было всего 42 «физкультурника», и не все из них оказались «неутомимыми». А среди «неутомимых» нашлось 12 таких, которые неутомимы и без спортивных тренировок.

В ыводы по подобной работе могут быть похожи по смыслу на п. 6 комментариев     (*)

Приложение  1

Критические значения критерия Пирсона («хи-квадрат»)

Число степеней свободы