ожиданий кардиоинтервала. (*)
Исходные данные:
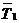 =0,60 с; D1 = 0,0075 с2
=0,60 с; D1 = 0,0075 с2
 = 0,76 с; D2 = 0,0111 с2
= 0,76 с; D2 = 0,0111 с2
n1 = n2 = 25
Нулевая гипотеза:
Н0: < М(Т1) = М(Т2) > (6)
Проверку выполняем по критерию Стьюдента.
Контрольное значение критерия Стьюдента, в общем случае:
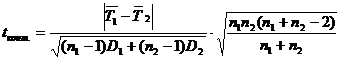 (7)
(7)
Поскольку n1 = n2 = n, то формула (7) упрощается, приводится к виду:
 (8)
(8)
Вычисления:
 t конт. = 5,88
t конт. = 5,88
Число степеней свободы:
L = n1 + n2 – 2 = 48
Принимаем уровень значимости a = 0,05. Для a = 0,05 и L = 48 из таблицы 8 или из приложения 2 получаем критическое значение t-критерия:
t кр = 2,01
Поскольку tконт > tкр., гипотеза о равенстве истинных средних М(Т1) = М(Т2) отбрасывается.
Вывод:
Доказано, что средневыборочные значения 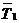 =0,60 с и
=0,60 с и  = 0,76 с отличаются значимо, с доверительной вероятностью р = 99,9% (но не 95%; см. комментарии, п.4). (**)
= 0,76 с отличаются значимо, с доверительной вероятностью р = 99,9% (но не 95%; см. комментарии, п.4). (**)
Комментарии к проверке гипотезы Н0: < М(Т1) = М(Т2) >
1. Напоминаем, что эта гипотеза проверяется с помощью критерия Стьюдента, поскольку в обеих выборках выполняется нормальный закон распределения.
2. Обращаем Ваше внимание на то, как хорошо расчетная формула (8) соответствует здравому смыслу. Из нее следует:
а) если 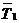 =
=  , то гипотеза (6) будет принята на любом уровне значимости, поскольку tконт. = 0.
, то гипотеза (6) будет принята на любом уровне значимости, поскольку tконт. = 0.
б) чем больше дисперсии D1 и D2, тем больше разброс в выборках, тем сильнее могут отличаться 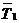 и М(Т1);
и М(Т1);  и М(Т2). Поэтому даже заметное отличие
и М(Т2). Поэтому даже заметное отличие 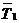 и
и  будет неубедительным. Увеличение знаменателя в формуле (8) работает на понижение tконт. То есть на принятие гипотезы М(Т1) = М(Т2)
будет неубедительным. Увеличение знаменателя в формуле (8) работает на понижение tконт. То есть на принятие гипотезы М(Т1) = М(Т2)
в) увеличение множителя  в формуле (8) «работает» на повышение tконт., на преодоление уровня критического значения крмтерия. То есть на то, чтобы отбросить гипотезу М(Т1) = М(Т2). И правильно делает. Потому что чем больше объем выборки, тем ближе
в формуле (8) «работает» на повышение tконт., на преодоление уровня критического значения крмтерия. То есть на то, чтобы отбросить гипотезу М(Т1) = М(Т2). И правильно делает. Потому что чем больше объем выборки, тем ближе 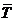 к истинному среднему М(Т). Даже очень малые разности
к истинному среднему М(Т). Даже очень малые разности  при больших по объему выборках будут приняты как значимые. Наоборот, при малых выборках даже заметные разности
при больших по объему выборках будут приняты как значимые. Наоборот, при малых выборках даже заметные разности  будут признаны не значимыми.
будут признаны не значимыми.
3. Приводим фрагмент таблицы критических значений t-критерия, достаточный для выполнения данной расчетной работы. Более полную таблицу
см. в приложении 2.
Таблица 9. Критические значения коэффициента Стьюдента.
| Число степеней свободы | Уровень значимости | |||||
| a = 0,10 | a = 0,05 | a = 0,02 | a = 0,01 | a = 0,005 | a = 0,001 | |
| L = 40 | 1,68 | 2,01 | 2,42 | 2,70 | 2,97 | 3,55 |
| L = 60 | 1,67 | 2,00 | 2,39 | 2,66 | 2,91 | 3,46 |
Для L = 48» 50 значения a определяются интерполяцией; как среднеарифметическое между значениями a для L = 40 и L = 60.
4. Приняв уровень значимости a = 0,05, мы согласились на вероятность ошибки первого рода, равную 5%. В нашем примере получено: tконт. =5,88, а для a = 0,05 tкр = 2,01, следовательно, tконт > tкр. Но ведь 5,88 не просто больше, а намного больше, чем 2,01. Посмотрев внимательно таблицу 8, можно заметить, что наше значение tконт = 5,88 превосходит даже то значение tкр, которое характерно для уровня значимости a = 0,001 (оно равно 3,55). Следовательно, в нашем примере фактическая ошибка при отбрасывании гипотезы – не 5%, а менее 0,1%: значения 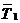 и
и  отличаются так существенно, что доверительная вероятность нашего вывода оказалась р = 99,9%, а не 95%. Но это – в нашем примере. А как у Вас?
отличаются так существенно, что доверительная вероятность нашего вывода оказалась р = 99,9%, а не 95%. Но это – в нашем примере. А как у Вас?
5. Громоздкая полноразмерная формула (7) для вычисления контрольного значения критерия обрадует того исследователя, у которого, к примеру, контрольная выборка по объему большая, а экспериментальная – пока что маленькая.
Проверка гипотезы о равенстве
математических ожиданий дисперсий. (*)
Н0: < М(D1) = М(D2) >
Проверку выполняем по критерию Фишера (F-критерий)
Выборочные дисперсии:
D1 = 0,0075 с2; D2 = 0,0111 с2
Контрольное значение критерия:
Fконт. = 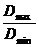
Здесь Dmax – наибольшее из чисел D1 и D2, а Dmin – наименьшее из них.
Fконт. = 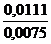 = 1,48.
= 1,48.
Принимаем уровень значимости a = 0,05. По таблице 10 или по табл. приложения 3 для числа степеней свободы L1 = L2 = n – 1 = 24 и a = 0,05 находим Fкр. = 1,98.
Получили Fконт. = 1,48; Fкр. = 1,98.
Так как Fконт. < Fкр., гипотеза о равенстве истинных значений дисперсий принимается. На уровне значимости a = 0,05 отличие выборочных дисперсий D1 и D2 не значимо. Степень ритмичности сердечных сокращений в ходе диагностической процедуры не изменилась. (**)
Комментарии к проверке гипотезы о равенстве дисперсий.
1. Проверка данной гипотезы по критерию Фишера оправданна, поскольку в обеих выборках выполняется нормальный закон распределения.
2. Дисперсия вычисляется по значениям исходной случайной величины, представленной выборкой табл. 1 или 2. Поэтому она является новой случайной величиной, и ее выборочное значение – это то, что вычисляется по элементам выборки. Это более или менее точная оценка истинной дисперсии, которую можно было бы вычислить теми же приемами, но по всей генеральной совокупности, и этот результат назывался бы «математическое ожидание дисперсии». Имеем то, что можем – выборочную дисперсию D, а хотелось бы знать M(D).
3. Обратите внимание: величина Fконт. = 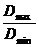 показывает, во сколько раз числитель превосходит знаменатель. В нашем примере дисперсии отличаются в 1,49 раза, и тем не менее их отличие признано не значимым.
показывает, во сколько раз числитель превосходит знаменатель. В нашем примере дисперсии отличаются в 1,49 раза, и тем не менее их отличие признано не значимым.
4. Необходимые для данной работы критические значения F-критерия приведены в табл.10 и в приложении 3. Если выборки отличаются по объему, необходимые таблицы можно найти в литературе по математической статистике.
Таблица 10. Критические значения F-критерия
| Число степеней свободы | Уровень значимости | ||
| a = 0,05 | a = 0,01 | a = 0,001 | |
| L = n – 1 = 24 | 1,98 | 2,66 | 3,74 |
Выводы по работе (вариант 1). (*)
Методами математической статистики проанализированы данные кардиоинтервалографии в двух состояниях пациента:
состояние 1 – до введения обзидана;
состояние 2 – через 40 минуть после введения обзидана.
Данные о состояниях пациента представлены двумя выборками объемом по 25 элементов.
По числовым характеристикам выборок и по гистограммам были сформулированы предварительные выводы и проведена их проверка с помощью статистических критериев.
Предварительные выводы подтвердились частично. Окончательные выводы об изменении работы сердца
1. Доказано, что с доверительной вероятностью р = 99,9% среднее значение кардиоинтервала значимо возросло от уровня 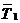 = 0,60 ± 0,04 с до уровня
= 0,60 ± 0,04 с до уровня  = 0,76 ± 0,05 с. Частота сердечных сокращений, соответственно, уменьшилась от 100 до 79 ударов в минуту.
= 0,76 ± 0,05 с. Частота сердечных сокращений, соответственно, уменьшилась от 100 до 79 ударов в минуту.
2. Предварительный вывод об изменениях дисперсии не подтвердился. На уровне значимости a = 0,05 значимых изменений дисперсии не установлено. Это означает, что степень ритмичности сердечных сокращений не изменилась. (**)
Предисловие к применению критерия Уилкоксона.
Если в хотя бы одной из Ваших выборок нормальный закон не выполняется, их сопоставление следует проводить с применением непараметрических критериев.
Статистический критерий называется НЕПАРАМЕТРИЧЕСКИМ, если для его применения не требуется предварительное знание о законах распределения случайных величин в выборках (и соответственно не требуется знание параметров этих распределений). Иначе говоря, непараметрические критерии применимы при любых законах распределения в выборках.
Непараметрическими из рассмотренных нами являются критерий Пирсона и критерий Шапиро-Уилка. Для вынужденного завершения расчетной работы №1 по сценарию №2 целесообразно воспользоваться непараметрическим критерием Уилкоксона.
Критерий Уилкоксона применяется для проверки гипотезы об однородности выборок.
Две выборки называются ОДНОРОДНЫМИ, если доказано, что они принадлежат к одной генеральной совокупности, то есть могут рассматриваться как две части одной генеральной совокупности. Принадлежность двух выборок к одной генеральной совокупности не означает, что выборки одинаковы, как написанные под копирку: ведь при их формировании одно из требований - это случайность выбора элементов. Признаком однородности выборок может служить близость значений характеристик выборок, большое сходство гистограмм.
В данной работе доказанная однородность двух выборок кардиоинтервала, полученных в ходе диагностической процедуры, означает, что в ходе обследования параметры работы сердца значимо не менялись, вместо двух ожидавшихся режимов его работы получился один, и в этом смысле диагностическая процедура оказалась не эффективной.
Гипотеза об однородности выборок формулируется как равенство функций распределения случайной величины (Т) в двух выборках:
Н0: < f(T1) = f(T2) >
Уилкоксон с соавторами предложили оценивать степень близости двух выборок по перемешанности чисел, представленных в этих выборках. Для этого из двух упорядоченных выборок строится единая возрастающая числовая последовательность, и подсчитывается количество ИНВЕРСИЙ – фактов вклинивания, внедрения чисел одной числовой последовательности в вереницу чисел другой последовательности.
Проверка гипотезы об однородности выборок 1 и 2. (*)
Нулевая гипотеза: Н0: < f(T1) = f(T2) >
Проверка выполняется по критерию Уилкоксона.
Таблица 11 Единая упорядоченная последовательность
| Инверсии 2®1 | Выборка 1 | Выборка 2 | Инверсии 1®2 | ||
| 0 | 1 | 0,43 | |||
| 0,44 | 1 | 1×1 = 1 | |||
| 21×1 = 21 | 21 | 0,45 0,46 0,48 0,51 0,54 0,55 0,56 0,58 0,59 0,60 0,60 0,61 0,62 0,62 0,64 0,64 0,65 0,65 0,65 0,66 0,66 | |||
| 0,67 0,68 0,70 | 3 | 3×22 = 66 | |||
| 2×4 = 8 | 2 | 0,71 0,71 | |||
 0,79 0,79
| 0,72 0,72 0,72 0,72 0,74 0,74 0,74 0,75 0,75 0,76 0,76 0,78 0,78 0,78 0,79 0,83 0,83 0,84 0,85 0,87 1,10 | 20 | 20×24 = 480 | ||
| å И2®1 = 29 | å И1®2 =547 | ||||
Объемы уточненных выборок: n/1 = 24; n/2 = 24
Расчет контрольного значения U-критерия:
А.) Uконт. = 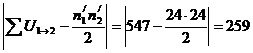
Б) Uконт. = 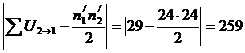
Получены совпадающие результаты, что говорит об отсутствии ошибок при подсчете инверсий.
Критическое значение U-критерия:
Uкр =  , для уровня значимости a = 0,05 по таблице12 принимаем Z = 1.96
, для уровня значимости a = 0,05 по таблице12 принимаем Z = 1.96
Uкр = 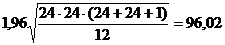
Имеем Uконт = 259; Uкр = 95,05.
Вывод: поскольку Uконт > Uкр, то на уровне значимости a = 0,05 гипотеза об однородности выборок 1 и 2 отбрасывается, т.е. выборки признаются неоднородными. (**)






