1. Таблица имеет 5 рабочих столбцов, сообразно числу классовых интервалов (классов) k = 5. j – номер класса; j = 1,2,3,4,5.
2. Средняя точка Тj j-го класса вычисляется как среднее арифметическое значений его левой и правой границ, установленных в п. 5 таблицы 4.
3. В строке 3 – разность между числами строки 2 и средневыборочным значением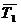 
из таблицы 3.
4. В строке 4 – разности строки 3, деленные на s1. Переменная 
введена здесь из соображений удобства.
5. В строке 5 записывается взятый со знаком «минус» и деленный на два квадрат чисел строки 4.
6. Вычисления строки 6 выполняются с помощью калькулятора с функциями.
7. В строке 7 сначала вычисляется множитель 
, а затем – пять значений плотности вероятности f j нормального закона распределения. Фактически, они вычисляются, следуя предположению: М(Т) = 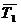; s = s1. Назовем их теоретическими значениями плотности вероятности.
8. Строка 8 – это выборочные значения плотности вероятности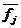 
9. В строке 9 записываются разности f j и 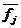, т.е. отличия между теоретическими и выборочными значениями плотности вероятности. Эти разности могут оказаться положительными или отрицательными.
10. В строке 10 записываются квадраты разностей строки 9. Эти числа не отрицательны.
11. В строке 11 вычисляются пять значений величины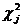 
, являющихся локальными (местными) оценками несоответствия распределений 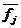и f j друг другу. Их сумма в строке 12 является контрольным значением критерия «хи – квадрат»
12. Приводим фрагмент большой таблицы критических значений критерия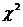 
(табл.6). Большая таблица приведена в приложении 1.
Таблица 6. Критические значения критерия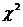
| Число степеней свободы | Уровень значимости, a | ||||
| 0,3 | 0,1 | 0,05 | 0,01 | 0,001 | |
| L = 1 L = 2 | 1,07 2,41 | 2,71 4,61 | 3,84 5,99 | 6,63 9,21 | 10,8 13,8 |
Пригодившееся в нашем примере значение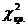 
выделено жирным шрифтом.
Комментарии к таблице 5.
1. Число степеней свободы L - это количество независимых данных в пятерке исходных. Это можно понимать так: если известны любые две величины 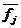,сумма 
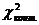и двухпараметрическая формула (3), то три других могли бы быть восстановлены расчетным путем, если бы они вдруг потерялись. То есть объективно независимы только L = 2 величины.
2. Уровень значимости a - это вероятность ошибки в предстоящих результатах, выводах, заключениях. Величину a исследователь назначает себе сам, сообразуясь со спецификой решаемой задачи. Наиболее часто в литературе встречаются значения a = 0,1; 0,05; 0,01; 0,001. В переводе на проценты этот ряд выглядит так: a = 10%; 5%; 1%; 0,1%.
3. В математической статистике различают ошибки двоякого рода:
Ошибки первого рода – это ошибки непринятия гипотезы в обстоятельствах, когда на самом деле ее следовало принять.
Ошибки второго рода – это ошибки принятия гипотезы в обстоятельствах, когда на самом деле ее принимать не следовало.
При беглом чтении различия между этими типами ошибок можно недооценить. Но вдумайтесь: отнести здорового к категории больных – это гуманнее, чем отнести больного к категории здоровых. Признав здорового за больного, Вы отправите его на дополнительное обследование, и там-то все и прояснится. Признав больного здоровым, Вы откажете ему в помощи, на которую он вправе рассчитывать.
В данной расчетной работе уровень значимости a - это вероятность ошибки первого рода. В медицинских комиссиях призывных пунктов военкоматов тяготеют к ошибкам второго рода..
4.. Если установлено, что хотя бы в одной из Ваших выборок нормальный закон распределения не выполняется, Вы лишаетесь возможности применить при последующем анализе простые и эффективные критерии Стьюдента и Фишера. Но с другой стороны, факт «ненормальности» распределения более информативен, чем может показаться на первый взгляд. Нормальное распределение случайной величины – это результат совместного несогласованного действия множества факторов, ни один из которых не является доминирующим. Если Вы убеждаетесь, что в Вашей выборке нормальный закон не выполняется, значит среди случайных факторов, определивших эту выборку, есть доминирующие, а это уже - призыв к действиям по их выявлению.
5. Для проверки нормальности распределения в выборках может использоваться конкурент критерия Пирсона – критерий Шапиро-Уилка, рассмотренный в трех нижеследующих разделах данного пособия.
