Гистограммы: рекомендации по графике.

1. Гистограммы целесообразно строить на миллиметровой бумаге (миллиметровке).

Применение миллиметровки – один из элементов рационализации жизни студента, инженера, исследователя. Любой график строится на миллиметровке быстрее и точнее, чем на обычной бумаге.

2. В данном задании строятся две гистограммы, сообразно двум состояниям пациента. Должны быть приняты меры, предельно упрощающие их сопоставление. Следуйте нашему примеру на рисунке 1.

3. Гистограммы размещаются одна под другой, с одинаковой масштабной разбивкой по оси абсцисс.

4. По оси ординат масштабная шкала должна начинаться с нуля: ведь за пределами гистограмм плотность вероятности имеет значение f(T) =0.

5. Шкалы по оси ординат гистограмм 1 и 2 могут отличаться друг от друга.

6. Поскольку значения случайной величины Т измеряются в секундах (с), то значения плотности вероятности f(T), откладываемые по ординате, имеют размерность = с^-1. Почему? Потому что произведение плотности вероятности f на ширину основания h имеет смысл относительной частоты попадания случайной величины Т в этот классовый интервал, а она, как и вероятность, величина безразмерная.

Выводы по гистограммам. (*)

1. Центр гистограммы 2 находится правее, чем центр гистограммы 1. Это означает, что в ходе диагностической процедуры среднее значение кардиоинтервала, по-видимому, возросло. Частота сердечных сокращений, соответственно, уменьшилась.

2. Гистограмма состояния 2 заметно шире, чем гистограмма 1. Это означает, что в состоянии 2 сердце пациента стало работать менее ритмично.

3. Гистограмма 2 имеет форму, близкую к симметричной. Это может означать, что в состоянии 2 случайная величина Т подчиняется нормальному закону распределения.

4. Гистограмма 1 асимметрична. По-видимому, в этом состоянии пациента нормальный закон распределения не выполняется. (**)

Комментарии к выводам по гистограммам.

1. Центр гистограммы – центр тяжести гистограммы – это такая точка на оси Т, в которой надо мысленно поставить опору под гистограммой, чтобы при этом ее левая и правая части друг друга уравновешивали.

2. Пункты 1 и 2 выводов по гистограммам совпадают с выводами, сделанными по таблице 3. По другому и быть не могло: выборки заявили о себе сначала языком «сухой цифири» точечных характеристик, а затем – языком графических образов - гистограмм.

3. «Сортировка» элементов выборок по классовым интервалам (классам) дала возможность сформулировать пункты 3 и 4 выводов.

4. При обсуждении симметричности гистограмм, имелась в виду похожесть гистограммы на график плотности вероятности нормального закона распределения: максимум – в центре и понижение высоты ступеней к краям.

5.. Осторожный, предположительный характер выводов по гистограммам (или по табл. 3) соответствует тому факту, что объем исходных выборок невелик. Более того, каждую из исходных выборок мы расщепили на пять.

Статистическая гипотеза. План дальнейшей работы.

Математический анализ, результатом которого должно стать подтверждение, уточнение или опровержение полученных предварительных выводов, составляет содержание следующего этапа работы. В математической статистике сложилась технология такого анализа, которая называется ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.

Ситуация с выдвижением статистической гипотезы может складываться следующим образом. Вы выполняете эксперимент, в ходе которого Вы получили две выборки данных, соответствующие двум стадиям исследования или двум группам исследуемых объектов. Предположим, что некоторая характеристика A, подсчитанная по выборке 1, оказалась равной , а по выборке 2 получилось значение , такое, что > . Для проверки этого утверждения формулируем нулевую гипотезу:

Н₀: < М (А ₁) = М (А ₂) > (1)

Здесь в стрельчатых скобках – суть гипотезы: предполагаемое РАВЕНСТВО математических ожиданий случайных величин А ₁ и А ₂ Мы высказали недоверие результату > , полученному по выборкам, поскольку выборка - это далеко не генеральная совокупность. Если будет признано, что результаты и объективно достаточно близки, гипотеза (1) будет принята. В противном случае она будет отброшена, а неравенство > будет признано доказанным, ЗНАЧИМЫМ.

Степень близости и можно оценивать, обсуждая, насколько близка к нулю разность 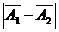, или насколько близко к единице отношение / ; возможны и другие способы сопоставления. Внимание: величины типа 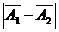; / - это новые случайные величины, основанные на «старых», представленных исходными выборками.

Случайные величины типа / , или 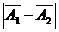, и т.п., составляют основу СТАТИСТИЧЕСКИХ КРИТЕРИЕВ ИСТИННОСТИ статистических гипотез. Их разработка связана с именами таких выдающихся математиков, как У.С. Госсет (псевдоним – Стьюдент), Р.Э. Фишер, К. Пирсон, Уилкоксон (Wilkokson), Колмогоров, и др. Разработанные ими статистические критерии носят их имена. Каждый из критериев предназначен для проверки статистических гипотез определенного типа. Иначе говоря, статистические критерии имеют специализацию по типам задач, решаемых с их помощью.

Однако вернемся к нашему мысленному эксперименту. Мы выдвинули гипотезу (1), и выяснили, что ее проверка может быть выполнена с помощью некоторого С – критерия. (Criterion – (греч.) – средство для суждения). Средством для суждений по С – критерию будет расчетная формула, в которую надо подставить средневыборочные значения и . Результаты вычислений дадут некоторый числовой результат С_конт. – контрольное значение критерия С по данным Вашего эксперимента. Теперь надо выяснить, то ли этот числовой результат достаточно мал, то ли он слишком велик.

Для этого необходимо: для своих объемов выборок n₁ и n₂, и для уровня ошибки, который Вы сочтете приемлемым, найти критическое значение С – критерия – величину С_кр.Это делается с помощью таблиц или вспомогательных формул, полученных при разработке С – критерия.

Если окажется, что С_конт. ≤ С_кр., то гипотеза (1) принимается. Тем самым принимается знак равенства в формулировке (1) гипотезы. Результат > не отменяется, но признается неубедительным, НЕ ЗНАЧИМЫМ.

Если окажется, что С_конт. > С_кр, то гипотеза (1) не принимается (отбрасывается). Ваш результат > признается доказанным, ЗНАЧИМЫМ.

По рассмотренной схеме работают все статистические критерии.

Выбор приемлемого уровня ошибки обсудим на конкретных ситуациях нашего примера выполнения расчетной работы.

Теперь, приняв к сведению принцип «доверяй, но проверяй!», можно обсудить план дальнейших разумных действий по выполнению расчетной работы.

А план таков (тезисы):

1. Для выборки, имеющей менее симметричную гистограмму, необходимо выполнить проверку гипотезы о ее принадлежности к нормально распределенной генеральной совокупности.

2. Если окажется, что в менее симметричной выборке нормальный закон выполняется, то в другой, более симметричной, он тоже выполняется.

3. Если в обеих выборках выполняется нормальный закон, то по любой из выборок можно определять границы доверительного интервала для математического ожидания М(Т).

4. Если в обеих выборках выполняется нормальный закон, то ранее полученные предварительные выводы можно проверить с помощью t-критерия Стьюдента и F-критерия Фишера. По результатам проверки соответствующих гипотез, предварительные выводы корректируются, формулируются выводы окончательные.

5. Если гипотеза о нормальном законе хотя бы в одной из двух выборок не выполняется, применять t-критерий и F-критерий нельзя. Вместо этого выборки анализируются с помощью непараметрического U-критерия Уилкоксона.

Таким образом, какие методы анализа применять можно, а какие – нельзя в условиях Ваших исходных данных, придется решать самостоятельно. Ну, а как применять эти методы, мы покажем ниже.

Логике предложенного плана действий соответствует следующая блок-схема: