1. Ширина доверительного интервала dТ является мерой неопределенности той информации, которую способна предоставить нам выборка. Мы хотели бы знать истинное среднее, а получаем его оценку в виде доверительного интервала. В нашей выборке 1 значение М(Т) может оказаться любым числом из диапазона 0,56 – 0,64 с, а с вероятностью 5% - даже за пределами этого диапазона.
2. Обращаем Ваше внимание на хорошее соответствие расчетной формулы (5) для dТ здравому смыслу:
а) чем больше разброс в выборке (s), тем больше и неопределенность dТ;
б) чем больше объем выборки n, тем меньше неопределенность dТ.
3. Коэффициент Стьюдента всегда больше единицы, и показывает, во сколько раз необходимо увеличить результат вычисления величины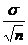 
при Ваших объеме выборки и уровне значимости. При малых выборках коэффициент Стьюдента может превосходить 10: малая выборка – большая ширина доверительного интервала, низкая точность.
4. Значения коэффициента Стьюдента для числа степеней свободы L = 24 приведены в таблице 8, являющейся фрагментом таблицы приложения 2.
Таблица 8. Значения коэффициента Стьюдента.
| Число степеней свободы | Уровень значимости | |||||
| a = 0,20 | a = 0,10 | a = 0,05 | a = 0,02 | a = 0,01 | a = 0,001 | |
| L = 24 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | 3,75 |
6. В нашем примере доверительные интервалы не перекрывают друг друга. При других исходных данных могло получиться иначе: могло быть их частичное перекрытие и даже полное поглощение одного доверительного интервала другим. В пределах участка числовой оси, принадлежащего обоим интервалам, возможно попадание как М(Т1), так и М(Т2), и следовательно в пределах зоны перекрытия доверительных интервалов возможно все, что угодно: М(Т1) < М(Т2), М(Т1) = М(Т2), М(Т1) > М(Т2). В этих обстоятельствах отличие срерневыборочных значени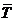й 
1 и 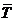2 следует признать не значимым.
7. На уровне значимости a = 0,05 мы получили результат:
М(Т1) = 0,60 ± 0,04с. Приведем два примера другого выбора уровня значимости.
Если бы наш выбор уровня значимости был a = 0,20, то границы доверительного интервала по выборке 1 оказались бы М(Т1) = 0,60 ± 0,02с. А при выборе a = 0,001 получаем М(Т1) = 0,60 ± 0,07с
Первое из этих двух заключений производит впечатление результата с повышенной точностью, но оно верно лишь с доверительной вероятностью р = 80%.
Второе заключение это результат низкой точности, но зато с повышенной доверительной вероятностью р = 99,9%.
Исследователи авантюрного склада тяготеют к первому варианту, перестраховщики – ко второму.
Выбор a = 0,05 встречается в литературе очень часто и воспринимается как «золотая середина»: в выводы «закладывается» допустимая ошибка первого рода в 5% по вероятности.
Далее приводится продолжение примера выполнения расчетной работы №1, если допустимо следовать «сценарию № 1»
