1. Расчетные формулы (2) и (3) параметров а и b уравнения линейной регрессии получены, следуя методу наименьших квадратов (МНК). В основе МНК –требование: сумма квадратов отклонений всех точек исходных данных от графика уравнения y = b x + a должна быть наименьшей из всех возможных. Это обеспечивается выбором параметров a и b..
2. Графики на рисунке 1: пунктирная прямая – по интуиции и сплошная прямая – по уравнению регрессии, - могут отличаться друг от друга достаточно заметно, и чем меньше значение коэффициента корреляции, тем заметнее.
3. При вычислениях параметра b примите к сведению, что числитель формулы (2) совпадает с числителем формулы (1), а знаменатель – с подкоренным выражением одного из квадратных корней той же формулы.
4. Зависимость у(х), получаемую в виде уравнения регрессии, не следует сразу рассматривать как описание причинно-следственной связи. Большая неосторожность трактовать одну из исходных величин как причину, а вторую как следствие лишь потому, что первая оказалась обозначенной буквой х, а вторая – буквой у.
5 Ценность уравнения регрессии часто состоит в том, что для любого значения х уравнение дает возможность вычислить значение среднестатистической нормы показателя у.
А иногда представление результатов исследований в виде уравнения регрессии и его графика – это «элегантная математическая упаковка» вашей интеллектуальной продукции. Ведь обсуждать уравнения и их графики несравненно проще и убедительнее, чем таблицы выборок.
6. Публикуя уравнение регрессии, Вы обязательно должны указать диапазоны значений х и у исходных данных. И применять уравнение следует именно в этих диапазонах.
Применение уравнения за пределами диапазонов значений исходных данных называется ЭКСТРАПОЛЯЦИЕЙ. Она иногда все же используется как способ получения осторожного прогноза.
Выводы по расчетной работе. (*)
1. Установлено, что у детей в возрасте до 14 лет, больных псориазом, существует значительная положительная линейная связь между концентрацией в крови микроэлементов: железо (величина х) и цинк (величина у). Коэффициент корреляции r = 0,55
2. Эта связь описывается уравнением линейной регрессии у = 0,23х + 9,12
где х (мкмоль/л) – концентрация Fe
у (мкмоль/л) – концентрация Zn
3. Данное уравнение получено на основе результатов анализов у больных в возрасте от 2 до 14 лет для диапазонов значений концентраций:
по Fe: от 0 до х = 41 мкмоль/л
по Zn: от 0 до у = 20 мкмоль/л (**)
Анализ сопряженности качественных признаков. Введение.
В медицине большую ценность могут представлять качественные признаки.
Они не имеют строго количественной меры. Но и качественные признаки нуждаются в оценках уровня выраженности качеств. Подобные оценки необходимы и при описании фактов, и при их анализе.
К простейшим шкалам для качественных признаков относится номинальная шкала. В номинальной шкале имеются некоторые общепринятые градации, и тогда оцениваемый признак можно, по преобладанию, отнести к одной из этих градаций (номинировать в этой градации). Например, темперамент можно обсуждать в номинационной шкале с четырьмя градациями: холерик, сангвиник, флегматик, меланхолик.
Предельно простой частный случай номинационной шкалы – альтернативная (дихотоническая; ди – два). В ней – всего две градации: наличие какого-то качества и отсутствие этого качества: да или нет; болен или не болен; быть или не быть…
Измерения, в обсуждаемом смысле, на более высоком уровне обеспечивают порядковые шкалы качественных признаков. Такие шкалы сближают идеологии измерений качественных и количественных признаков. Так, в широко применяемых ранговых шкалах имеется упорядоченная возрастающая последовательность уровней оценки качественного признака. Пример порядковой шкалы: пятибальная шкала оценки знаний.
Сопряженность качественных признаков – это свойство, которое можно уподобить корреляционной связи признаков, имеющих количественное измерение. В обоих случаях имеется в виду, что при изменении одного из признаков обнаруживается устойчивая тенденция к изменению другого. И в обоих случаях установление подобной связи еще не означает обнаружение причинно-следственной связи между признаками.
В двух следующих разделах приведен пример анализа сопряженности двух альтернативных признаков, с последующими пояснениями и рекомендациями. Метод разработан К. Пирсоном.
Анализ сопряженности качественных признаков. Пример. (*)
Пример ситуации. Было проведено исследование влияния занятий спортом на утомляемость к концу рабочего дня молодых выпускников вуза. Обследовалась группа выпускников численностью n = 200 человек. Каждому предлагалась анкета с вопросами:
1. Занимаетесь ли Вы спортом систематически?
2. Испытываете ли Вы состояние психического или физического утомления к концу рабочего дня?
По обоим вопросам ожидаемые ответы: «да» или «нет». Результаты обследования приведены ниже, в табл. 1.
Использованы следующие обозначения:
признак А – отношение к спорту:
да, занимаюсь – символ А
нет, не занимаюсь – символ 
признак В – утомляемость:
да, утомляюсь – символ В
нет, не утомляюсь – символ 
Таблица 1. К расчету показателей сопряженности
.
| Занятия спортом (А) Утомление (В) | A (+) |
 (-)
| ∑ |
| B (+) | a=36 | b=124 | a+b=160 |
 (-)
| c=28 | d=12 | c+d=40 |
| ∑ | a+c=64 | b+d=136 | n=200 |
Расчеты параметров сопряженности
1. Коэффициент ассоциации (связи):
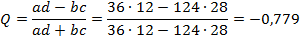(1)
2. Коэффициент контингенции (сопряженности):
(2)
Проверка статистической значимости параметров
1. Предполагаем, что ассоциация (связь) в данных табл. 1 отсутствует, и проверяем нулевую гипотезу Н0: < Q = 0 >. Проверка - по критерию Пирсона. Контрольное значение критерия Пирсона:
При числе степеней свободы L = 1 на уровне значимости α = 0.05 из таблицы приложения 1 имеем критическое значение критерия Пирсона:
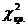= 3.84
Поскольку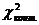 
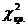> , нулевая гипотеза отбрасывается, и результат Q = - 0.779 признается статистически значимым на уровне значимости α = 0.05.
2. Предполагаем, что в данных табл. 1 контингенция (т.е. сопряженность) отсутствует. Проверяем нулевую гипотезу Н0: < Ф = 0 >. Контрольное значение критерия Пирсона:
Т.к. число степеней свободы и принятый уровень значимости не изменились, критическое значение критерия Пирсона - прежнее:
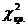= 3.84
Поскольку 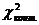> 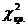, нулевая гипотеза отбрасывается, и результат Ф = - 0.423 признается статистически значимым на уровне значимости α = 0.05.
Фактически же полученные значения Q и Ф статистически значимы и на уровне значимости α = 0.001, на котором 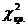= 10.83. (**)
