1. Коэффициент корреляции r – величина, имеющая область возможных значений – интервал [-1; 1]; или, что то же самое, | r | £ 1.
2. Если, нанеся исходные данные на график, Вы видите такое расположение точек, что с ростом величины х вторая переменная – величина у – несмотря на разброс точек, в среднем возрастает – то такому положению дел соответствует положительное значение коэффициента корреляции. Если же увеличение одной из переменных отслеживается уменьшением другой, то коэффициент корреляции будет величиной отрицательной.
Мы говорим о возрастании или убывании лишь как о тенденциях, которые угадываются на фоне большого разброса точек исходных данных. Подобные тенденции обнаруживаются лишь при наличии достаточно большого исходного материала. На нашем графике рисунка 1 мы выделили точки (3) и (7) исходных данных. Если бы были только эти две точки, можно было бы думать, что с ростом х величина у уменьшается, и это было бы ошибкой.
3. Простейшая математическая форма описания подобных тенденций – это описание возрастания или убывания по закону прямой линии. Такие связи называются линейными связями (именно так; линейными, а не прямолинейными)
4. Коэффициент корреляции говорит о наличии линейной связи между двумя переменными, и ничего не говорит о наличии или отсутствии связей более сложных, нелинейных.
5. Пунктирная прямая, проведенная на рисунке 1, отражает наше интуитивное понимание характера зависимости y = f (x). Чем ближе коэффициент корреляции к единице, тем легче провести такую усредняющую прямую. Ну, а при r = +1 или r = -1 провести прямую не составило бы никакого труда: прямая прошла бы через все точки, или, что то же самое, все точки оказались бы на одной прямой.
6. Связь между переменными х и у, которую мы обсуждали как тенденцию, как изменения «в среднем», называется корреляционной. При | r | = 1 корреляционная линейная связь становится функциональной связью. Функциональная зависимость между переменными - частный случай корреляционной связи.
7. Чем ближе к нулю значение коэффициента корреляции, тем линейная связь слабее.
8. Вычислив значение коэффициента корреляции, Вы можете оценить силу связи между х и у в сложившихся наименованиях этой «силы» с помощью табл. 2.
Таблица 2.Характеристики линейной корреляционной связи
| Значения модуля коэффициента корреляции | Качественная характеристика линейной связи |
| | r | £ 0,3 0,3 < | r | £ 0,5 0,5 < | r | £ 0,7 0,7 < | r | £ 0,9 0,9 < | r | £ 1 | слабая умеренная значительная сильная очень сильная |
9. Отсутствие линейной связи между х и у не исключает существования более сложных, нелинейных связей.
10. Наличие связи между величинами х и у, более сложной, чем линейная, можно ощутить по характеру расположения точек (х; у) исходных данных. Приведем пример ситуации, когда наличие нелинейной связи весьма ощутимо. На рисунке 2 точками нанесены данные о частоте пульса у детей различного возраста, имевших врожденно пониженную частоту сердечных сокращений (ЧСС). Данные предоставлены А.Я. Волковым (кафедра факультетской педиатрии СПбГПМА). Видно, что с увеличением возраста ЧСС уменьшается, но
| Частота пульса; уд/мин | 110 105 100 95 90 85 80 75 70 |

|
0 2 4 6 8 10 12 14 16
Возраст; лет Рис. 2
Уравнение линейной регрессии. (*)
Зависимость у(х) будем описывать уравнением регрессии y = a + b x,
здесь b – коэффициент регрессии, a – свободный член
 (2)
(2)
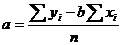 (3)
(3)
Вычисления:

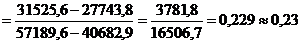

Получено уравнение линейной регрессии у = 0,23х + 9,12
Таблица для построения графика этого уравнения по двум точкам:
| х | у = 0,23х + 9,12 |
| 4 40 | у = 0,23×4 + 9,12 = 10,04 у = 0,23×40 + 9,12 = 18,32 |
По этим данным построен график уравнения регрессии (сплошная прямая на рис. 1)
(**)













