Шапиро-Уилка.
Критерий Пирсона широко применяется для проверки различных гипотез. Но именно при решении задач о проверке нормальности распределения заинтересованная общественность в последние годы стала отдавать предпочтение критерию Шапиро-Уилка. Тому есть следующие причины. Во-первых, некоторые ограничения возможностей критерия Пирсона связаны с тем, что в теоретическую модель нормального распределения закладываются выборочные оценки математического ожидания и среднеквадратичного отклонения исследуемой случайной величины, а это может быть оправданно лишь при выборках большого объема. Во-вторых, как уже отмечалось, при получении гистограммы исходная выборка фактически распадается на несколько малых, сообразно числу ступеней гистограммы. Доверие к этим малым выборкам очень низкое именно в силу их малости.
Критерий Шапиро-Уилка оказался хорошим конкурентом критерия Пирсона при проверке нормальности распределения именно в малых и средних выборках.
Чтобы показать, как проводится проверка нормальности распределения с применением критерия Шапиро-Уилка, мы взяли из исходной выборки 1 (табл.1) десять первых элементов, и эту малую выборку проверили на нормальность по Шапиро-Уилку. Как удалось убедиться, вывод о нормальном распределении в сравнительно большой выборке 1 объемом n1 = 25, полученный по Пирсону, подтверждается анализом малой части этой выборки объемом 10 элементов, выполненным по Шапиро-Уилку на том же уровне значимости α = 0.05.
Пример применения критерия Шапиро-Уилка. (*)
Исходные данные - выборка значений кардиоинтервала объемом n = 10.
Задача: проверка гипотезы о выполнении нормального закона распределения в заданной выборке
Нулевая гипотеза:
Н0: <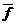 
(Т1) = f(Т1) >
Здесь 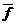(Т1) – эмпирическое распределение случайной величины Т1
f(Т1) – теоретическое распределение случайной величины Т1 в соответствии с нормальным законом распределения. Параметры М(Т) и s не известны.
1
Проверку гипотезы выполняем по критерию Шапиро-Уилка
Таблица 7. К вычислению контрольного значения W -критерия.
| № | T1j | Упорядоченное T1j | k | ∆T | α n , k, | ∆T α n , k, |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0.83 | 0.44 | 1 | 0.66 | 0.5739 | 0.3788 |
| 2 | 0.72 | 0.68 | 2 | 0.15 | 0.3291 | 0.0494 |
| 3 | 0.68 | 0.70 | 3 | 0.08 | 0.2141 | 0.0171 |
| 4 | 0.75 | 0.72 | 4 | 0.03 | 0.1224 | 0.0036 |
| 5 | 0.74 | 0.74 | 5 | 0.01 | 0.0399 | 0.0004 |
| 6 | 0.44 | 0.75 | b=å∆T α n , k, | 0.4493 | ||
| 7 | 1.10 | 0.75 | ||||
| 8 | 0.70 | 0.78 | ||||
| 9 | 0.75 | 0.83 | ||||
| 10 | 0.78 | 1.10 | ||||
Контрольное значение критерия Шапиро-Уилка:
Критическое значение критерия, на уровне значимости α = 0.05:
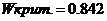
Т.к.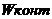 
> 
, нулевая гипотеза принимается.
Вывод: с доверительной вероятностью p = 0.95 в проанализированной выборке выполняется нормальный закон распределения. (**)
Пояснения к вычислениям по таблице 7.
1. В столбце 2 помещена анализируемая выборка, В столбце 3 все элементы этой выборки размещены в порядке возрастания.
2. В столбце 4 пронумерованы, а в столбце 5 – записаны разности ∆ k. Они вычисляются следующим образом: из последнего элемента упорядоченной выборки вычитается первый, затем из предпоследнего – второй, и т. д.. Если объем выборки – число нечетное, то центральный элемент упорядоченной выборки в образовании разностей не участвует (т.е. если бы объем выборки был бы 11, а не 10, то все равно было бы образовано 5 разностей).
3. В столбце 6 помещены значения коэффициентов α n , k, взятые в приложении 4. В таблице приложения выбирается столбец коэффициентов, соответствующий объему анализируемой выборки n и количеству получившихся разностей k. В нашем примере n = 10, k = 5.
4. В столбце 7 – произведения чисел столбцов 5 и 6, а внизу – их сумма b, необходимая для вычисления контрольного значения критерия W.
5. Таблица критических значений критерия Шапиро-Уилка приведена в приложении 5.
ВНИМАНИЕ: при работе с критерием Шапиро-Уилка нулевая гипотеза принимается, если контрольное значение критерия больше критического (а не меньше, как обычно в подобных ситуацияхпри работе с другими критериями).
Предисловие к вычислениям границ доверительных интервалов.
1.Процедура определения границ доверительного интервала для математического ожидания случайной величины достаточно проста. Но применять ее можно в случае, если в выборке выполняется нормальный закон распределения. В литературе встречается дополнение: «… или близкие к нему распределения».
2. Установлено, что случайные погрешности измерений подчиняются нормальному закону распределения, «или близки к нему».
5. В нашем примере оказалось оправданным определение границ доверительных интервалов для истинного среднего в обеих выборках. Будут ли оправданны такие действия в условиях Ваших исходных данных, – Вам предстоит выяснить. Но все же после этого, в интересах обретения навыков, следует определить границы доверительных интервалов для условий Вашего индивидуального задания по приведенной ниже методике.
