В работе анализируется случайная величина Т – кардиоинтервал. Его обозначения в двух состояниях пациента: Т1 и Т2 .
Исходные данные.
1) Выборка 1 значений Т1; объем: n1 = 25, до введения обзидана; см. табл. 1.
2) Выборка 2 значений Т2; объем: n2 = 25, через 40 минут после введения обзидана; см. табл. 2.
Таблица 1. Выборка 1.
| (i) | T1.i | Упорядоченные T1.i | Класс j | DT1.j = T1.i - 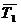
| DT1.i2 (c2) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 0,51 0,71 0,65 0,64 0,62 0,64 0,66 0,62 0,55 0,46 0,43 0,60 0,60 0,65 0,59 0,45 0,48 0,65 0,66 0,79 0,56 0,54 0,58 0,71 0,61 | 0,43 0,45 0,46 0,48 0,51 0,54 0,55 0,56 0,58 0,59 0,60 0,60 0,61 0,62 0,62 0,64 0,64 0,65 0,65 0,65 0,66 0,66 0,71 0,71 0,79 | 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 5 | -0,17 -0,15 -0,14 -0,12 -0,09 -0,06 -0,05 -0,04 -0,02 -0,01 0 0 0,01 0,02 0,02 0,04 0,04 0,05 0,05 0,05 0,06 0,06 0,11 0,11 0,19 | 0,0289 0,0225 0,0196 0,0144 0,0081 0,0036 0,0025 0,0016 0,0004 0,0001 0 0 0,0001 0,0004 0,0004 0,0016 0,0016 0,0025 0,0025 0,0025 0,0036 0,0036 0,0121 0,0121 0,0361 |
| å | ----- | 14,96 | ----- | ----- | 0,1808 |
Таблица 2. Выборка 2.
| (i) | T2.i | Упорядоченные T2.i | Класс j | DT2.j = T2.i - 
| DT2.i2 (c2) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 0,83 0,72 0,68 0,75 0,74 0,44 1,10 0,70 0,76 0,75 0,78 0,72 0,67 0,85 0,72 0,79 0,83 0,87 0,72 0,76 0,78 0,74 0,74 0,84 0,78 | 0,44 0,67 0,68 0,70 0,72 0,72 0,72 0,72 0,74 0,74 0,74 0,75 0,75 0,76 0,76 0,78 0,78 0,78 0,79 0,83 0,83 0,84 0,85 0,87 1,10 | 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 | -0,32 -0,09 -0,08 -0,06 -0,04 -0,04 -0,04 -0,04 -0,02 -0,02 -0,02 -0,01 -0,01 0 0 0,02 0,02 0,02 0,03 0,07 0,07 0,08 0,09 0,11 0,34 | 0,1024 0,0081 0,0064 0,0036 0,0016 0,0016 0,0016 0,0016 0,0004 0,0004 0,0004 0,0001 0,0001 0 0 0,0004 0,0004 0,0004 0,0009 0,0049 0,0049 0,0064 0,0081 0,0121 0,1156 |
| å | ----- | 19,10 | ----- | ----- | 0,2663 |
Характеристики первого состояния:
Средневыборочное значение:

Дисперсия выборки:

Среднеквадратичное отклонение в выборке:

Средняя частота сердечных сокращений:

Характеристики второго состояния:
Средневыборочное значение:

Дисперсия выборки:

Среднеквадратичное отклонение в выборке:
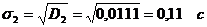
Средняя частота сердечных сокращений:

(**)
Указания к расчетам по таблицам 1 и 2.
1. Занести в столбец 2 таблиц значения кардиоинтервалов Ti и Т2 из карты индивидуального задания. Значения кардиоинтервалов рекомендуется представлять с округлением до двух значащих цифр после запятой. Округление сопряжено с некоторой потерей точности (в данном случае – порядка 1%), но уменьшает трудоемкость вычислений примерно в полтора раза.
На всякий случай, округления иллюстрируем примерами:
0,528с» 0,530с = 0,53с; 0,632с» 0,630с = 0,63с;
0,725с» 0,730с = 0,73с; 1,095с» 1,100с = 1,10с
2. В столбце 3 разместить данные столбца 2 в порядке возрастания. Повторяющиеся значения Ti помещать одно под другим.
У Вас будет возможность убедиться, что с упорядоченными выборками работать удобнее, чем с неупорядоченными.
3. Вычислить сумму всех элементов столбца 3. Результат записать в этом же столбце, в нижней строке, обозначенной å (сумма).
4. Вычислить средневыборочные значения кардиоинтервалов 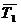 и
и  . Точность вычислений – две значащие цифры после запятой.
. Точность вычислений – две значащие цифры после запятой.
Столбец 4 на данном этапе работы не заполняется; к нему предстоит вернуться позже. Переходите к столбцу 5.
Дальнейшие пояснения относятся к табл.1, но таковы же они и для табл.2, где будет Т2 вместо Т1 ,  вместо
вместо 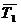 , и т.п.
, и т.п.
5. Заполнить столбец 5 значениями разности между числами Ti столбца 3 и средневыборочным значением 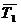 : DTi = Ti -
: DTi = Ti - 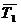 . В верхней половине столбца 5 значения DTi отрицательные (поскольку здесь Ti <
. В верхней половине столбца 5 значения DTi отрицательные (поскольку здесь Ti < 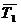 ), а в нижней части – положительные. Суммирование данных столбца 5 не предусмотрено, но может быть выполнено «факультативно» для самопроверки: сумма чисел столбца 5 должна быть равна нулю, или очень близка к нулю, если при вычислениях производились округления.
), а в нижней части – положительные. Суммирование данных столбца 5 не предусмотрено, но может быть выполнено «факультативно» для самопроверки: сумма чисел столбца 5 должна быть равна нулю, или очень близка к нулю, если при вычислениях производились округления.
6. Заполнить столбец 6: числа DTi столбца 5 возвести в квадрат.
Целесообразно параллельное заполнение столбцов 5 и 6: вычисление D Ti, запись результата в столбец 5, и тут же – вычисление квадрата этого числа, с записью в столбец 6.
Для сохранения принятого уровня точности результатов анализа, значения DTi2 вычисляются с точностью до четырех значащих цифр после запятой.
7. Вычислить сумму элементов столбца 6. Результат записать в этом же столбце, в нижней строке å.
8. Вычислить значение дисперсии выборки D1. Точность вычислений – четыре значащие цифры после запятой.
9. Вычислить значение среднеквадратичного отклонения s1. Точность вычислений – две значащие цифры после запятой. (Возводя DTi в квадрат, мы «уходим» на четыре значащие цифры после запятой, выполняя обратное действие – извлечение квадратного корня, - возвращаемся к прежнему уровню точности).
10. Вычислить значение средней частоты сердечных сокращений (ЧСС). Разумное округление результатов вычислений – до целочисленных значений количества сокращений в минуту.
11. Полученные результаты свести в таблицу 3 и провести их сравнительный анализ; пример – смотри ниже.
Характеристики выборок. (*)
Таблица 3.
| Состояние пациента: | до введения абзидана | через 40 минут после введения абзидана |
| № выборки | 1 | 2 |
| Средневыборочное значение кардиоинтервала | 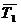 = 0,60с = 0,60с
|  =0,76с =0,76с
|
| Дисперсия выборки | D1 = 0,0075с2 | D2 = 0,0111с2 |
| Среднеквадратичное отклонение | s1 = 0,09с | s2 = 0,11с |
| Частота сердечных сокращений | (ЧСС)1 = 100 1/мин | (ЧСС)2 = 79 1/мин |
Предварительные выводы по характеристикам выборок
.
1. В ходе обследования среднее значение кардиоинтервала 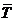 возросло (
возросло ( >
> 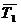 ), а ЧСС, соответственно, уменьшилась. Обнаружено увеличение среднего кардиоинтервала в
), а ЧСС, соответственно, уменьшилась. Обнаружено увеличение среднего кардиоинтервала в  /
/ 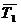 = 0,76/0,60 = 1,27 раза. ЧСС уменьшилась в 1,27 раза.
= 0,76/0,60 = 1,27 раза. ЧСС уменьшилась в 1,27 раза.
2. В ходе обследования средневыборочная дисперсия возросла (D2 > D1). Обнаружено увеличение дисперсии в D2 / D1 = 0,0111/0,0075 = 1,49 раза. По-видимому, в состоянии 2 сердце пациента стало работать менее ритмично. (**)
Пояснения по предварительным выводам.
1. Если бы характеристики, представленные в таблице 3, были получены не по
выборкам, а по генеральным совокупностям, их можно было бы считать не предварительными, а окончательными. Но они получены по выборкам скромных объемов n1 = n2 = 25, и разумная степень доверия к ним и к результатам их сопоставления будет установлена математически.
2. ЧСС и средний кардиоинтервал 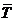 взаимно обратны: ЧСС ~
взаимно обратны: ЧСС ~  ;
; 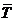 ~
~  . Чем больше
. Чем больше 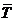 , тем меньше ЧСС, и наоборот. Таково же соотношение частоты и периода в теории колебаний.
, тем меньше ЧСС, и наоборот. Таково же соотношение частоты и периода в теории колебаний.
3. Изменения дисперсии D отслеживаются изменениями среднеквадратичного отклонения s, но – в ослабленном числовом выражении: ведь s =  , так что если дисперсия увеличится в 4 раза, то s тоже увеличится, но в
, так что если дисперсия увеличится в 4 раза, то s тоже увеличится, но в  = 2 раза.
= 2 раза.
4. Указывая, во сколько раз изменилась (возросла или уменьшилась) та или иная величина, мы сравниваем два ее значения через дробь, подставляя в числитель большее из этих значений: количество раз (разов?) не может быть меньше одного раза!
Гистограмма: введение.
Характеристики выборок, сведенные в табл. 3, относятся к категории точечных характеристик, поскольку получена группа чисел, а всякому числу соответствует, в качестве геометрического образа, некоторая точка на числовой оси. Точечные характеристики отражают очень важную информацию о свойствах выборок, и при этом весьма лаконичны. Коротко и ясно!
Но существует и другая форма представления свойств выборок, основанная на интервальных оценках, т.е. на примыкающих друг к другу интервалах числовой оси и наглядной графической иллюстрацией того, в каких интервалах случайная величина встречалась чаще, в каких – реже, а в каких – вообще не наблюдалась. Подобные картинки называются гистограммами.
Гистограммы являются украшением любого сообщения. Они информативны и наглядны. Навыки их построения Вам предстоит обрести. Необходимые подготовительные процедуры к построению гистограмм отражены в табл. 4.
Как выглядят гистограммы, видно на рис.1. ГИСТОГРАММА – столбчатая диаграмма – один из видов графического изображения статистического распределения случайной величины. Гистограмма представляет собой совокупность смежных прямоугольников с основаниями одинаковой протяженности. Основание прямоугольника соответствует некоторому диапазону значений случайной величины. Своей высотой ступени показывают:
1. в каких диапазонах значений случайная величина наблюдалась чаще, а в каких – реже.
2.) в каких диапазонах значений случайная величина будет наблюдаться чаще, а в каких - реже, если экспериментальное исследование данной случайной величины продолжить или повторить. В этом – прогностическая ценность гистограмм.
Но поскольку гистограмма строится по выборке, а не по генеральной совокупности, полного доверия к ней и к выводам по ней быть не должно. Если из той же генеральной совокупности взять повторную выборку того же объема и для нее тоже построить гистограмму, то эти две гистограммы будут похожи, но не идентичны, а при малых выборках они могут оказаться и не очень-то похожими друг на друга.
Таблица 4. К построению гистограмм (*)
| Параметр | Выборка 1. | Выборка 2. | ||||
| 1 | Объем выборки | n1 = 25 | n2 = 25 | |||
| 2 | Tmax | 0,79с | 1,10с | |||
| Tmin | 0,43с | 0,44с | ||||
| Размах R = Tmax - Tmin | 0.36c | 0.66c | ||||
| 3 | Количество классовых интервалов k» log2n | k1 = 5 | k2 = 5 | |||
| 4 | Ширина классовых интервалов: 
| h1 = | h2 = | |||
| 5 | Номер j класса | Границы классовых интервалов | ||||
| 1 2 3 4 5 | 0,43 – 0,502 0,502 – 0,574 0,574 – 0,646 0,646 – 0,718 0,718 – 0,79 | 0,44 – 0,572 0,572 – 0,704 0,704- 0,836 0,836 – 0,968 0,968 – 0,11 | ||||
| 6 | Номер j класса | Частота nj попаданий в классы | ||||
| 1 2 3 4 5 | 4 4 9 7 1 | 1 3 15 5 1 | ||||
| Проверка: (å) = 25 | (å) = 25 | (å) = 25 | ||||
|
7 | Номер j класса | Относительная частота uj = nj / n | ||||
|
| ||||||
| 1 2 3 4 5 | 0,16 0,16 0,36 0,28 0,04 | 0,04 0,12 0,60 0,20 0,04 | ||||
| Проверка: (å) = 1 | (å) = 1,00 | (å) = 1,00 | ||||
| 8 | Номер j класса | Плотность вероятности | ||||
| 1 2 3 4 5 | 2,22 2,22 5,00 3,89 0,56 | 0,30 0,91 4,55 0,52 0,30 | ||||
| Проверка: (å)×h = 1 | 13,89 × 0,072 = 1 | 7,58 × 0,132 = 1 | ||||
Гистограммы.
Состояние 1


 6
6
| |
 5
5
 4
4
| |
 3
3
 |
 2
2
| |
 Т1; с
Т1; с








 0
0
0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1
Состояние 2


 6
6
 5
5
 |
 4
4
 3
3
 2
2



 1
1  Т2;с
Т2;с








 0
0
0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 (**)
Пояснения к таблице 4.
1. В разделе 2 таблицы 4 значения Tmax и Tmin - это последний и первый элементы упорядоченной выборки табл. 1 или табл.2.
2.Размах R = Tmax - Tmin является простейшей мерой разброса данных в выборке. Дисперсия D – более «строгая» мера разброса.
3. В разделе 3 устанавливается количество классовых интервалов (классов), на которые будет разбит большой интервал R
Схема разбивки интервала R:
классы
 |







 1 2 3 4 5
1 2 3 4 5 
Т


 Tmin Tmax
Tmin Tmax
R = Tmax - Tmin
Количество классов k = 5 соответствует рекомендательной формуле: k» log2n, где n – объем выборки. Количество классов k – целое число. Знак «»» в приведенной формуле следует понимать как «равно, с округлением до ближайшего целого». В нашем примере принимается k = 5, поскольку log225 = 4,67» 5.
Однако на приведенную рекомендательную формулу для количества классов не следует молиться.. Встречаются ситуации, когда вместо рекомендуемых k = 5 приходится принимать, например, k = 3 в связи с малой «населенностью» отдельных классов.
4. Ширина h классового интервала в k = 5 раз меньше, чем размах выборки. Рекомендуем величину h вычислять с точностью до трех значащих цифр после запятой.
5. В разделе 5 границы классовых интервалов – это указание координат их начала и конца. Они устанавливаются пятью последовательными шагами h к значению Т; начиная от Tmin. Вычисления начинаются от Tmin и через пять шагов заканчиваются на Tmax
5А. Теперь, зная границы классовых интервалов, необходимо заполнить столбцы 4 таблиц 1 и 2, указав в них для каждого элемента упорядоченной выборки номер j классового интервала (класса), в который этот элемент попадает.
6. В разделе 6 частота nj – это количество элементов, попавших в каждый из пяти классов. Проще говоря, это число единиц, двоек, троек, и т.д. в столбце 4 таблицы 1 или 2.
В проверочной строке убедитесь, что нет потерявшихся или лишних элементов.
7. В разделе 7 значения частоты nj предыдущего раздела переведены в относительные частоты. Для этого числа, полученные в разделе 6, делятся на n = 25. Ценность полученных при этом данных весьма велика: ОТНОСИТЕЛЬНАЯ ЧАСТОТА СОБЫТИЯ и ВЕРОЯТНОСТЬ СОБЫТИЯ – понятия очень близкие. Относительная частота, подсчитанная по генеральной совокупности – это вероятность. Или по-другому: вероятность приблизительно равна относительной частоте.
В проверочной строке убедитесь, что целое (единица) равно сумме ее дробных долей.
8. В разделе 8 осуществляется переход от значений относительной частоты (раздел 7) к значениям плотности вероятности как фундаментальной характеристики случайной величины. И снова арифметика очень простая: достаточно поделить значения относительной частоты предыдущего раздела на ширину h классового интервала.
В проверочной строке – требование (å fj) × h = 1, что соответствует так называемому УСЛОВИЮ НОРМИРОВКИ. Смысл его – в следующем: вероятность того, что случайная величина (Т) принимает какое-нибудь из своих возможных значений (не важно, какое) в пределах интервала R, равна единице, как вероятность достоверного события.





 = 0.072c
= 0.072c = 0.132c
= 0.132c

