В инженерно-технологическую академию
1. Решить уравнение 
2. Решить неравенство 
3. Решить уравнение 
4. Решить уравнение 
5. Найти все значения p, при которых уравнение  не имеет корней.
не имеет корней.
6. В конус вписана пирамида,  В основании пирамиды лежит треугольник с углами
В основании пирамиды лежит треугольник с углами 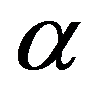 и
и  . Найти объем конуса.
. Найти объем конуса.
Решения
1. Решить уравнение 
Решение
Найдем область допустимых значений переменной:
 .
.
Преобразуем уравнение. Для этого перенесем  из левой части уравнения в правую, чтобы получить в обеих частях уравнения неотрицательные выражения, а затем возведем обе части уравнения в квадрат.
из левой части уравнения в правую, чтобы получить в обеих частях уравнения неотрицательные выражения, а затем возведем обе части уравнения в квадрат.
 ,
,
 . Правая часть уравнения неотрицательна при
. Правая часть уравнения неотрицательна при  , что совпадает с областью допустимых значений переменной. Возведем обе части уравнения в квадрат, получим:
, что совпадает с областью допустимых значений переменной. Возведем обе части уравнения в квадрат, получим:
 .
.
Оба корня входят в область допустимых значений и являются решениями уравнения.
Ответ:  .
.
2-й способ
Положим  .
.
Подставим в уравнение, получим: u - v = 1.
Получим систему уравнений:

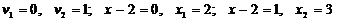 .
.
Ответ:  .
.
2. Решить неравенство 
Решение
Область допустимых значений:  .
.
Заметим, что  , т. е. выражения
, т. е. выражения  и
и  - взаимно обратные. Из равенства
- взаимно обратные. Из равенства  выразим
выразим  .
.
Неравенство примет вид:  .
.
Показательная функция с основанием 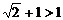 является возрастающей, значит,
является возрастающей, значит,  .
.
Квадратный трехчлен 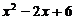 имеет отрицательный дискриминант, равный D = -20 < 0, значит, при всех значениях
имеет отрицательный дискриминант, равный D = -20 < 0, значит, при всех значениях  он принимает положительные значения и тогда, полученное неравенство равносильно неравенству:
он принимает положительные значения и тогда, полученное неравенство равносильно неравенству:
 .
.
Ответ:  .
.
3. Решить уравнение 
Решение
Область допустимых значений:  .
.
Преобразуем уравнение:  .
.
Полученное уравнение равносильно совокупности двух систем:
(1)  и (2)
и (2)  - эта система корней не имеет.
- эта система корней не имеет.
Ответ:  .
.
Внимание! Ошибочное преобразование!
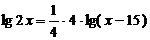 ,
,  .
.
Область допустимых значений этого уравнения "сузилась" и стала равна промежутку:  . В результате возможна потеря корней, что и произошло в данном случае.
. В результате возможна потеря корней, что и произошло в данном случае.
Уравнение  корней не имеет, хотя данное уравнение, как установлено выше, имеет корень x = 5.
корней не имеет, хотя данное уравнение, как установлено выше, имеет корень x = 5.
4. Решить уравнение 
Решение
Преобразуем уравнение, для чего используем следующие тригонометрические формулы:  и
и 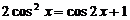 . Получим уравнение:
. Получим уравнение:
 .
.
Полученное уравнение равносильно совокупности уравнений:

Ответ: 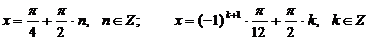 .
.
5. Найти все значения p, при которых уравнение  не имеет корней.
не имеет корней.
Решение
В первую очередь, выясним, будет ли иметь решение уравнение, когда его первый коэффициент равен нулю:  Уравнение примет вид:
Уравнение примет вид:  В этом случае уравнение корней не имеет, значит, значение
В этом случае уравнение корней не имеет, значит, значение  удовлетворяет условию задачи.
удовлетворяет условию задачи.
Теперь, в дальнейших рассуждениях, будем предполагать, что 
Преобразуем уравнение. Для этого положим  получим уравнение
получим уравнение 
Полученное уравнение не будет иметь корней в двух случаях:
1-й случай, когда дискриминант уравнения отрицателен 
2-й случай, когда уравнение имеет два отрицательных корня.
Рассмотрим каждый из этих случаев.
1-й случай. Найдем дискриминант и определим значения p, при которых он будет отрицателен:

 (см. рис. 73),
(см. рис. 73),

Рис. 73

2-й случай. Во-первых, уравнение должно иметь корни, что произойдет при 
Во-вторых, оба корня должны быть отрицательными. Чтобы выяснить, при каких значениях p это произойдет, преобразуем это уравнение к приведенному:

По теореме Виета, произведение корней равно свободному члену  а их сумма второму коэффициенту с противоположным знаком:
а их сумма второму коэффициенту с противоположным знаком: 
Чтобы оба корня были отрицательны, необходимо и достаточно, чтобы свободный член был положительным, а второй коэффициент, взятый с противоположным знаком - отрицательным. Получим систему:

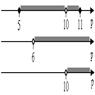
Рис. 74
 (см. рис. 74).
(см. рис. 74).
Объединяя множества, полученные из первого и второго случаев, а также, помня, что при p = 10 уравнение также не имеет решений, получаем множество, при котором уравнение не имеет корней: 
Ответ: 
6. В конус вписана пирамида,  В основании пирамиды лежит треугольник с углами
В основании пирамиды лежит треугольник с углами 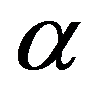 и
и  . Найти объем конуса.
. Найти объем конуса.
Решение

Рис. 75
1. Пусть R - радиус окружности основания конуса, H = SO - высота конуса и высота пирамиды, VК - объем конуса, VП - объем пирамиды (см. рис. 75).
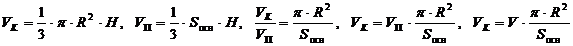 .
.
2. Таким образом, чтобы найти объем конуса, необходимо найти площадь треугольника в основании пирамиды. Применим к треугольнику теорему синусов, но прежде, найдем величину третьего угла треугольника:  .
.
По теореме синусов:  ,
,
 .
.
3. Площадь треугольника равна
 .
.
4. Найдем объем конуса
 .
.
Ответ:  .
.






