При x = 3, получим:  значит x = 3 является корнем уравнения.
значит x = 3 является корнем уравнения.
Ответ: 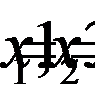
2-й способ
Положим  тогда
тогда  Получим систему уравнений, из которой исключим x:
Получим систему уравнений, из которой исключим x: 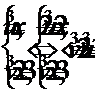
Чтобы получить второе уравнение системы, замени в данном уравнении 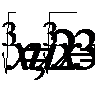 и
и  , получим уравнение:
, получим уравнение:

Из двух уравнений составим систему и решим ее:
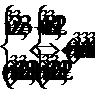
Решим полученное уравнение: 



Последнее уравнение равносильно совокупности уравнений:

Ответ: 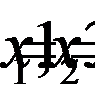
4. Решить уравнение: 
Решение
Область допустимых значений переменной найдем из решения системы неравенств (рис. 23):

|  Рис. 23
Рис. 23
|
Отсюда получаем  или
или 
Преобразуем уравнение:
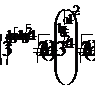

 так как, из области допустимых значений следует, что x > 1, то
так как, из области допустимых значений следует, что x > 1, то  а значит числитель и знаменатель дроби можно разделить на x + 1, получим уравнение:
а значит числитель и знаменатель дроби можно разделить на x + 1, получим уравнение: 
При  Возведем обе части полученного уравнения в квадрат:
Возведем обе части полученного уравнения в квадрат:

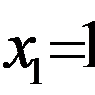 не входит в область допустимых значений и не является корнем уравнения, - это посторонний корень.
не входит в область допустимых значений и не является корнем уравнения, - это посторонний корень.
 входит в область допустимых значений и может быть корнем уравнения. Чтобы точно установить это, выполним проверку.
входит в область допустимых значений и может быть корнем уравнения. Чтобы точно установить это, выполним проверку.
Проверка

значит x = 3 является корнем уравнения.
Ответ: x = 3.
5. Доказать тождество 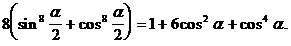
Доказательство
Преобразуем левую часть тождества:




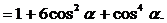 Тождество доказано.
Тождество доказано.
6. Образующая усеченного конуса наклонена к его основанию, имеющему радиус R, под углом 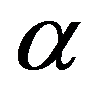 ; радиус другого основания равен r. Определить боковую поверхность усеченного конуса.
; радиус другого основания равен r. Определить боковую поверхность усеченного конуса.
Решение

Рис. 24
1. Площадь боковой поверхности определим по формуле:

2. Проведем BM перпендикулярно плоскости основания, тогда  по определению прямой, перпендикулярной плоскости. AM = R - r.
по определению прямой, перпендикулярной плоскости. AM = R - r.
Из  3.
3. 
Ответ: 
7. В круг радиуса r вписать прямоугольник с наибольшей площадью.
Решение

Рис. 25
1. Обозначим одну из сторон прямоугольника, возьмем AD = x.
2. Проведем OM  AD, тогда вторая сторона прямоугольника будет равна
AD, тогда вторая сторона прямоугольника будет равна 
3. Из 
4. Площадь прямоугольника будет равна 
5. Рассмотрим площадь, как функцию от x и найдем ее наибольшее значение на промежутке 

Найдем критические точки на промежутке 
 не входит в промежуток
не входит в промежуток 
При  значит функция возрастает.
значит функция возрастает.
При  значит функция убывает.
значит функция убывает.
В точке  функция имеет максимум. Значит наибольшая площадь прямоугольника будет при
функция имеет максимум. Значит наибольшая площадь прямоугольника будет при  и
и  т. е. это квадрат со стороной
т. е. это квадрат со стороной  и площадью
и площадью 
Ответ: 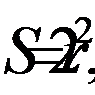 квадрат со стороной
квадрат со стороной  .
.
Вариант 7
1. Упростить: 
2. Найти все решения уравнения  , принадлежащих области определения функции
, принадлежащих области определения функции 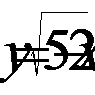
3. Решить уравнение: 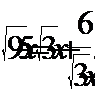
4. Решить уравнение: 
5. Решить уравнение: 
6. Два пешехода вышли одновременно навстречу друг другу и встретились через 3 ч. 20 мин. За какое время пройдет всё расстояние каждый из них, если первый пришел в то место, из которого вышел второй на 5 ч позже, чем второй пришел в то место, откуда вышел первый?
7. Основанием четырехугольной пирамиды служит ромб со стороной длины a и острым углом  . Каждая боковая грань наклонена к плоскости основания под углом
. Каждая боковая грань наклонена к плоскости основания под углом  Найти полную поверхность пирамиды.
Найти полную поверхность пирамиды.
Решения
1. Упростить: 
Решение
Выражение имеет смысл, если 
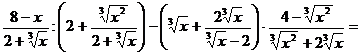


Ответ: 2, при  .
.
2. Найти все решения уравнения  , принадлежащих области определения функции
, принадлежащих области определения функции 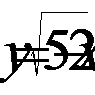
Решение
Найдем область определения функции. Выражение, находящееся под знаком квадратного корня должно быть неотрицательным:

Решим уравнение: 
Полученное уравнение равносильно совокупности двух систем:
(1)  и (2)
и (2) 
(1) 
Из двух корней, полученных в результате решения систем, только один входит в область определения функции, т. е. в промежуток  - это
- это 
Ответ: x = -4.
1. Решить уравнение: 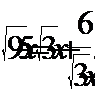
Решение
1-й способ
Найдем область допустимых значений переменной:

Возведем обе части уравнения в квадрат, получим:


 - не входит в область допустимых значений и не является корнем уравнения, это посторонний корень. Проверим корень x = -3.
- не входит в область допустимых значений и не является корнем уравнения, это посторонний корень. Проверим корень x = -3.
Проверка
При x = -3 получим: 
Ответ: 
2-й способ
Положим  тогда
тогда  отсюда можно исключить x и получить уравнение, содержащие переменные u и v.
отсюда можно исключить x и получить уравнение, содержащие переменные u и v.
Из системы уравнений исключим x:
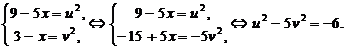
Подставляя значения  в первоначальное уравнение, получим:
в первоначальное уравнение, получим: 
Приходим к системе уравнений: 
Подставим значения u из второго уравнения в первое, получим:

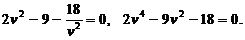 Это биквадратное уравнение. Положим
Это биквадратное уравнение. Положим  тогда придем к квадратному уравнению:
тогда придем к квадратному уравнению: 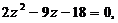 которое имеет два корня:
которое имеет два корня: 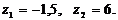
 не удовлетворяет условию
не удовлетворяет условию  и является посторонним корнем. Находим:
и является посторонним корнем. Находим: 
Ответ: 
4. Решить уравнение: 
Решение
Область допустимых значений: x > 0. Так как x находится в основании степени, то необходимо рассмотреть отдельно случай, когда x = 1.
При x = 1 получим:  значит,
значит,  тогда областью допустимых значений переменной будет являться множество:
тогда областью допустимых значений переменной будет являться множество: 
Прологарифмируем обе части уравнения по основанию 10:

 Пусть
Пусть  тогда получим:
тогда получим: 


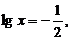
 Оба корня входят в область допустимых значений.
Оба корня входят в область допустимых значений.
Проверка
При  получим:
получим: 
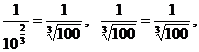 значит,
значит,  удовлетворяет уравнению.
удовлетворяет уравнению.
При  получим:
получим: 
значит,  удовлетворяет уравнению и является его корнем.
удовлетворяет уравнению и является его корнем.
Ответ: 
 .
.
5. Решить уравнение: 
Решение
Преобразуем уравнение

Положим  тогда получим квадратное уравнение:
тогда получим квадратное уравнение:

 - это уравнение не имеет решений, так как
- это уравнение не имеет решений, так как 


Ответ: 
6. Два пешехода вышли одновременно навстречу друг другу и встретились через 3 ч. 20 мин. За какое время пройдет всё расстояние каждый из них, если первый пришел в то место, из которого вышел второй на 5 ч позже, чем второй пришел в то место, откуда вышел первый?
Решение
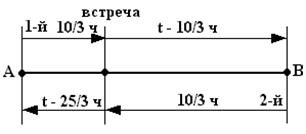
Рис. 26
t ч – время движения первого пешехода от A до B (см. рис. 26),
(t – 5) ч – время движения второго пешехода от B до A,
 и
и  км/ч – скорости первого и второго пешеходов соответственно,
км/ч – скорости первого и второго пешеходов соответственно,
 км – прошел до встречи 1-й пешеход,
км – прошел до встречи 1-й пешеход,
 км – прошел до встречи 2-й пешеход,
км – прошел до встречи 2-й пешеход,
 ч – время движения 1-го пешехода от встречи до прибытия в B,
ч – время движения 1-го пешехода от встречи до прибытия в B,
 ч – время движения 2-го пешехода от встречи до прибытия в A,
ч – время движения 2-го пешехода от встречи до прибытия в A,
 км – прошел после встречи второй пешеход.
км – прошел после встречи второй пешеход.
Составим 1-е уравнение

 км – прошел после встречи первый пешеход.
км – прошел после встречи первый пешеход.
Составим второе уравнение

Получим систему уравнений:

Разделим левые и правые части уравнений друг на друга, считая, что 
 получим:
получим: 

 не удовлетворяет условию задачи (иначе, не может на 5 ч позже придти первый в B, чем 2-й в A).
не удовлетворяет условию задачи (иначе, не может на 5 ч позже придти первый в B, чем 2-й в A).
10 ч – время движения первого пешехода, 5 ч – время движения второго.
Ответ: 10 ч, 5 ч.
7. Основанием четырехугольной пирамиды служит ромб со стороной длины a и острым углом  . Каждая боковая грань наклонена к плоскости основания под углом
. Каждая боковая грань наклонена к плоскости основания под углом  Найти полную поверхность пирамиды.
Найти полную поверхность пирамиды.
Решение

Рис. 27
1. Так как все боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом  , тогда высота пирамиды попадает в центр вписанной в основание окружности, а значит попадает в точку пересечения диагоналей ромба.
, тогда высота пирамиды попадает в центр вписанной в основание окружности, а значит попадает в точку пересечения диагоналей ромба.
2. Проведем  и соединим S и M,
и соединим S и M,  - по теореме о трех перпендикулярах, SM = h – апофема.
- по теореме о трех перпендикулярах, SM = h – апофема.
3. Из 

Рис. 28
4. Из 
5. 

Ответ: 
Вариант 8
1. Упростить:
2. Решить аналитически и графически уравнение:

3. Решить уравнение: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Пункт C расположен в 12 км от B вниз по течению реки. Рыбак отправился на лодке в пункт C из пункта A, расположенного выше пункта B. Через 4 часа он прибыл в C, а на обратный путь затратил 6 часов. Поставив мотор и тем самым увеличив скорость лодки относительно воды втрое, рыбак дошел от A до B за 45 минут. Определить скорость течения реки.
7. Найти конус наименьшего объема, описанный около шара радиуса R.
Решения
Упростить: 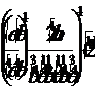
Решение
Выражение имеет смысл при 

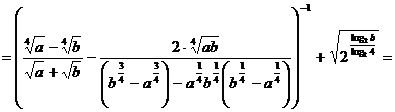

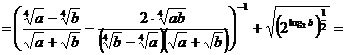

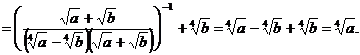
Ответ:  , при
, при  .
.
Решить аналитически и графически уравнение:

Решение
Аналитическое решение
Данное уравнение равносильно совокупности двух смешанных систем:
(1) 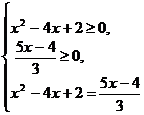 и (2)
и (2) 
Разложим квадратный трехчлен  на линейные множители. Для этого найдем его корни:
на линейные множители. Для этого найдем его корни:  Получим:
Получим:  .
.
Решим уравнение первой системы: 
Первая система станет такой:
 (1)
(1) 
Рис. 29
(1) 
Решим вторую систему:
 (2)
(2) 
Рис. 30
(2) 
Ответ: 






