Построим графики функций 
и 
. Абсциссы их точек пересечения будут являться решениями заданного уравнения.
1. Для построения графика функции , построим параболу 
, а затем выполним "зеркальное" отражение в оси Ox части параболы, лежащей ниже оси Ox.
Точки пересечения параболы с осью Ox: 
и 
.
Вершина параболы находится в точке с координатами:
2. Графиком функции является прямая, проходящая через точки:
3. Достаточно выполнить построения графиков справа от прямой x = 0,8, так как 
Выполним необходимые графические построения.
Отсюда, также находим, что 
Рис. 31
Ответ:
3. Решить уравнение: 
Решение
Й способ
Положим 
тогда 
.
Складывая левые и правые части этих равенств, получаем: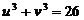 
.
Из данного уравнения, находим: 
.
Получим систему уравнений:
Решим первое уравнение системы:
.
.
Проверка
, значит,
- удовлетворяет уравнению.
, значит,
- удовлетворяет уравнению.
Ответ: 
.
Й способ
Возведем обе части уравнения в куб, получим:
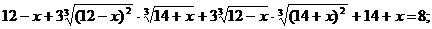
По условию 
тогда получим 
.
Ответ: .
4. Решить уравнение: 
.
Решение
Преобразуем уравнение:
.
Проверка
значит,
- удовлетворяет уравнению.
Ответ: .
5. Решить уравнение: 
.
Решение
Преобразуем уравнение:
, значит это уравнение не имеет решений.
Ответ: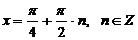 
.
6. Пункт C расположен в 12 км от B вниз по течению реки. Рыбак отправился на лодке в пункт C из пункта A, расположенного выше пункта B. Через 4 часа он прибыл в C, а на обратный путь затратил 6 часов. Поставив мотор и тем самым увеличив скорость лодки относительно воды втрое, рыбак дошел до от A до B за 45 минут. Определить скорость течения реки.
Решение
Пусть x км/ч – скорость течения реки,
y км/ч – скорость лодки в стоячей воде,
(y – x) км/ч – скорость лодки против течения реки,
Рис. 32
(y + x) км/ч скорость лодки по течению реки,
3(y – x) км/ч скорость лодки против течения с поставленным на нее мотором,
км – расстояние от A до B, которое прошла лодка с мотором, 
км – расстояние от A до C.
Получим систему уравнений:
Вычтем из второго уравнения первое, получим:
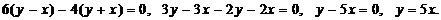
Подставим это значение y в первое уравнение системы, получим:
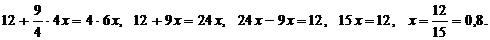
0,8 км/ч – скорость течения реки, 4 км/ч – скорость лодки в стоячей воде.
Ответ: 0,8 км/ч.
7. Найти конус наименьшего объема, описанный около шара радиуса R.
Решение
1-й способ
Рис. 33
1. O – центр описанного шара, H – высота конуса, r – радиус основания конуса, SO1 – высота конуса. Центр вписанного шара лежит на высоте конуса, поскольку рассматривается прямой круговой конус (по умолчанию в условии).
2. Пусть SO = x, R < x < 4R, тогда SO1 = x + r.
3. Из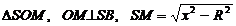 
. Из подобия треугольников SOM и SO1M следует, что 
4. Площадь основания конуса равна
Объем конуса 
5. Рассмотрим V как функцию от x и найдем ее наименьшее значение на промежутке R < x < 4R.
Найдем производную функции V(x)
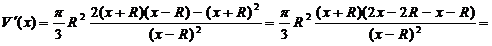
Критические точки: -R, 3R, R.
Рассмотрим только одну точку 3R, которая входит в промежуток R < x < 4R.
При R < x < 3R, 
- функция убывает на этом промежутке.
При 3R < x < 4R,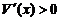 
- функция возрастает на этом промежутке.
Значит, в точке x = 3R функция имеет минимум.
6. Высота конуса H = x + R = 3R + R = 4R, радиус основания конуса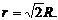 
Ответ: конус с радиусом основания 
и высотой H = 4R.
2-й способ
Пусть r, H, 
- радиус основания конуса, длина его высоты и величина угла наклона образующей к плоскости основания соответственно.
Имеем:
Введем новую переменную 
и продифференцируем полученную функцию, тогда 
В точке 
на интервале 
а на интервале 
в точке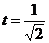 
функция имеет минимум, совпадающий с наименьшим значением функции на указанном промежутке 
Далее находим 
.
Ответ: .
Вариант 9
1. Упростить: 
2. Найти все решения уравнения 
принадлежащие области допустимых значений функции
3. Решить уравнение: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Лодка спустилась вниз по течению реки на 20 км., затем вернулась обратно, затратив 7 ч. На обратном пути на расстоянии 12 км. от начального пункта лодка поравнялась с плотом, который проплывал пункт отплытия лодки в момент ее отплытия. Определить скорость течения реки и скорость движения лодки вниз по течению.
7. Основанием пирамиды служит ромб, длины диагоналей которого равны 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и имеет длину 1 м. Найти площадь боковой поверхности пирамиды.
Решения
1. Упростить:
Решение
Выражение будет иметь смысл, если a > 0, 
.
Ответ: 1, при .
2. Найти все решения уравнения принадлежащие области допустимых значений функции
Решение
1. Найдем область определения функции 
. Логарифмическая функция имеет областью определения множество всех положительных чисел, значит 
. Это неравенство решим методом промежутков (рис. 34):
Рис. 34
Очевидно, что область определения 
.
2. Решим уравнение 
. Оно равносильно совокупности двух смешанных систем:
(1) 
и (2) 
(1) 
.
Оба корня входят в промежуток 
.
(2) 
.
Оба корня также входят в промежуток x < 0.
2-способ решения уравнения .
Положим |x| = y, 
тогда получим уравнение 
, которое имеет корни 
.
Найдем значения x: 
, 
.
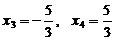Таким образом, уравнение имеет четыре корня. Установим, какие из корней входят в область определения функции .
.
Итак, только один корень входит в область определения функции: 
.
Ответ: .
3. Решить уравнение:
Решение
Область допустимых значений найдем из системы неравенств:
Преобразуем уравнение 
Положим 
, тогда получим квадратное уравнение:
не удовлетворяет условию y > 0 и не является корнем уравнения.
так как x > 1, тогда 
.
входит в область допустимых значений.
Проверка
, 
значит, удовлетворяет уравнению.
Ответ: .
4. Решить уравнение:
Решение
Областью допустимых значений переменной является множество всех действительных чисел 
, так как показательная функция 
принимает только положительные значения при любых значениях x.
Преобразуем уравнение
или 
Ответ: 
.
5. Решить уравнение:
Решение
Преобразуем уравнение, заменив 1 на квадрат суммы: 
,
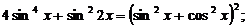
. Это уравнение однородное относительно sinx и cosx, причем 
.
Разделим обе части этого уравнения на 
, получим 
.
Положим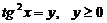 
, тогда получим квадратное уравнение:
. 
не удовлетворяет условию 
и является посторонним корнем.
Уравнение 
равносильно совокупности уравнений 
.
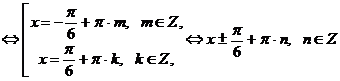Ответ: 
.
6. Лодка спустилась вниз по течению реки на 20 км., затем вернулась обратно, затратив 7 ч. На обратном пути на расстоянии 12 км. от начального пункта лодка поравнялась с плотом, который проплывал пункт отплытия лодки в момент ее отплытия. Определить скорость течения реки и скорость движения лодки вниз по течению.
Решение
Пусть x км/ч - скорость течения реки, y км/ч - скорость лодки в стоячей воде,
(y + x) км/ч - скорость лодки по течению реки,
(y - x) км/ч - скорость лодки против течения реки.
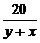ч - время движения лодки по течению реки,
ч - время движения лодки против течения реки.
Составим уравнение: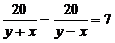 
.
x км/ч - скорость движения плота (равна скорости течения реки),
ч - время движения плота,
ч - время движения лодки до встречи с плотом.
Составим уравнение: 
.
Получим систему уравнений: 
Положим, что 
, получим
Из второго уравнения находим 
.
Подставим это значение y в первое уравнение, получим:
, тогда y = 7.
3 км/ч - скорость течения реки; 7 + 3 = 10 км/ч - скорость лодки по течению.
Ответ: 3 км/ч, 10 км/ч.
7. Основанием пирамиды служит ромб, длины диагоналей которого равны 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и имеет длину 1 м. Найти площадь боковой поверхности пирамиды.
Решение
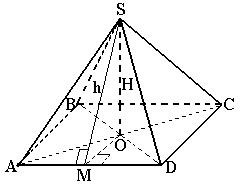
Рис. 35
1. 
где p - периметр основания, h - апофема (высота боковой грани), см. рис. 35.
2. Проведем 
, соединим S и M 
- по теореме о трех перпендикулярах, SM = h - апофема.
3. Рассмотрим основание. В 
м, DO = 3 м, (см. рис. 36):
Рис. 36
По теореме Пифагора 
м, тогда p = 20 м.
В 
, проведем из вершины прямого угла перпендикуляр OM на гипотенузу AD. AO - катет, AD - гипотенуза, AM - отрезок гипотенузы, прилежащий к катету AO. Каждый катет - средняя пропорциональная (средняя геометрическая) между всей гипотенузой и отрезком гипотенузы, прилежащем к этому катету.
Значит, 
, отсюда 
.
По теореме Пифагора из 
.
4. Из 
м.
5. 
м2.
Ответ: 
м2.
Вариант 10
1. Упростить:
2. Пусть 
и 
корни уравнения 
Вычислить 
3. Решить неравенство:
4. Решить уравнение:
5. Решить уравнение:
6. Из двух городов выехали одновременно навстречу друг другу два автомобиля. Первый за 3 ч прошел 0,08 всего расстояния между городами, а второй за 2,5 ч. 7/120 этого расстояния. Найдите (в км/ч) скорость второго автомобиля, если до места встречи первый прошел 800 км.
7. Боковая грань правильной треугольной пирамиды образует с плоскостью основания угол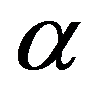 
, сумма длин высоты пирамиды и радиуса окружности, вписанной в основание пирамиды равна a. Найти объем пирамиды.
Решения
1. Упростить:
Решение
Выражение имеет смысл, если 
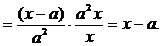
Ответ: 
, при 
2. Пусть и корни уравнения Вычислить
