Рис. 14
Ответ: 
4. Решить уравнение: 
Решение
Область допустимых значений переменной. Переменная под знаком логарифма должна быть положительной x > 0 (область определения логарифмической функции множество положительных действительных чисел).
В данном уравнении переменная находится в основании логарифма, значит необходимо установить, будет ли являться решением уравнения значение x = 1.
При x = 1 получим: 
значит 
Окончательно находим область допустимых значений переменной для данного уравнения: 
Преобразуем уравнение:
Положим 
тогда получим:
Проверка
При 
получим: 
значит, - корень уравнения.
При 
получим: 
значит является корнем уравнения.
Ответ: , .
5. Решить уравнение: 
Решение
Преобразуем уравнение: 
Полученное уравнение равносильно совокупности уравнений:
Второе уравнение совокупности 
решений не имеет, поскольку 
Первое уравнение решим как однородное. Разделим обе его части на 
в противном случае, из уравнения, получим, что и 
что невозможно). В результате деления на 
, приходим к уравнению:
Ответ: 
6. В основании пирамиды лежит ромб. Высота пирамиды проходит через центр ромба. Боковые грани пирамиды образуют углы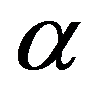 
и 
с диагоналями ромба. Найти угол наклона боковой грани к плоскости основания.
Решение
Рис. 15
1. Проведем 
соединим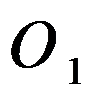 
с B и C, тогда 
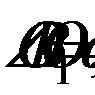так как 
является проекцией BO на боковую грань SBC. 
так как 
является проекцией OC на боковую грань SBC.
2. Обозначим OC = y, OB = x, тогда из 
3. Проведем 
в плоскости SBC, соединим O и M, 
- по теореме о трех перпендикулярах, значит 
- линейный угол двугранного угла между SBC и основанием пирамиды ABCD.
4. Рассмотрим 
- диагонали ромба пересекаются под прямым углом (рис. 16):
Рис. 16
5. Рассмотрим 
(рис. 17):
Рис. 17
6. Рассмотрим 
Ответ: 
7. Найти высоту конуса максимального объема, который можно вписать в шар радиуса R.
Решение
Рис. 18
1. Обозначим 
тогда высота конуса 
2. Из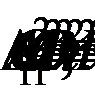 
3. 
4. Объем конуса равен 
5. Рассмотрим объем конуса, как функцию от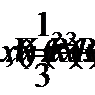 
где 
Найдем производную этой функции:
Найдем критические точки, 
- не входит в промежуток
При 
- функция возрастает.
При 
- функция убывает.
Значит, в точке 
функция имеет максимум, т. е. конус имеет максимальный объем.
Ответ: 
Вариант 5
1. Упростить: 
2. При каких значениях a разность корней уравнения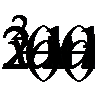 
равна их произведению?
3. Решить неравенство: 
4. Решить уравнение 
5. Решить уравнение: 
6. Два экскаватора производят работу. Если эту работу будет выполнять один первый экскаватор, то он может закончить ее на 8 ч. позже, чем оба вместе. Если эту работу будет выполнять один второй экскаватор, то он закончит ее на 4,5 ч позже, чем оба вместе. За какое время может выполнить эту работу каждый экскаватор в отдельности?
7. Стороны треугольника, лежащего в основании пирамиды равны 13, 14, 15 см. Двугранные углы при основании пирамиды равны по 450. Найти боковую поверхность пирамиды.
Решения
1. Упростить:
Решение
Выражение имеет смысл при 
Ответ: 3, при
2. При каких значениях a разность корней уравнения 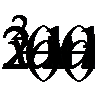равна их произведению?
Решение
Во-первых, найдем значения a, при которых уравнение вообще будет иметь действительные корни. Как известно, для этого дискриминант должен быть неотрицательным, т. е. больше нуля или равняться нулю:
при всех действительных значениях a, 
Пусть 
и 
- корни данного квадратного уравнения, тогда, по условию:
Для дальнейшего решения, необходимо преобразовать данное уравнение в приведенное, чтобы применить теорему Виета. Для этого разделим обе части уравнения на коэффициент при 
, т. е. на 2, получим: 
По теореме Виета: 
Получим систему уравнений, состоящую из трех уравнений:
Из третьего уравнения следует, что 
. Подставим это значение во второе уравнение, система примет вид:
Складывая левые и правые части первых двух уравнений, находим:
Вычитая из первого уравнения второе, получим:
Подставим значения и в третье уравнение системы, найдем a:
Ответ: при 
3. Решить неравенство:
Решение
Разложим квадратный трехчлен, находящийся в знаменателе дроби, на линейные множители: 
Преобразуем неравенство: 
Выражение, находящееся под знаком модуля, равно нулю при x = 3.
Получим два промежутка x < 3 и x > 3 (равенство 3 невозможно, так как при этом значении знаменатель обращается в нуль).
Решим неравенство на каждом из этих промежутков:
При x < 3 выражение x - 3 будет принимать отрицательные значения, значит "выйдет" из-под знака модуля с "минусом", получим неравенство:
Если еще учесть, что знаменатель не может быть равен нулю при 
тогда получим систему неравенств (рис. 19):
| 
Рис. 19
|
Находим решения системы: 
При x > 3 неравенство примет вид: 
Получим систему неравенств (рис. 20):
| 
|
Эта система решений не имеет. Рис. 20
Ответ:
4. Решить уравнение:
Решение
Область допустимых значений переменной найдем из решения системы неравенств: 
Преобразуем уравнение:
не входит в область допустимых значений и не является корнем уравнения. Проверим второй корень.
Проверка
x = 3 - является корнем уравнения.
Ответ: x = 3.
5. Решить уравнение:
Решение
Преобразуем уравнение: 
Полученное уравнение - однородное,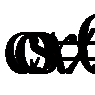 
Разделим обе части уравнения на 
приходим к уравнению:
Ответ: 
6. Два экскаватора производят работу. Если эту работу будет выполнять один первый экскаватор, то он может закончить ее на 8 ч позже, чем оба вместе. Если эту работу будет выполнять один второй экскаватор, то он закончит ее на 
ч позже, чем оба вместе. За какое время может выполнить эту работу каждый экскаватор в отдельности?
Решение
Пусть за xч - выполнит всю работу 1-й экскаватор, работая один,
yч - выполнит всю работу 2-й экскаватор, работая один,
1 - вся работа
тогда 
- делает в час 1-й экскаватор, его производительность,
- делает в час 2-й экскаватор, его производительность,
- делают в час два экскаватора, работая вместе,
ч - выполнят всю работу оба экскаватора, работая вместе.
По условию, получим систему уравнений: 
Вычтем из первого уравнения второе, получим: 
Преобразуем первое уравнение системы:
Получим новую систему уравнений: 
Значения 
не удовлетворяют условию задачи.
Остаются значения 
Ответ: за 14 ч - первый экскаватор выполнит всю работу, работая один;
за 10,5 ч - второй экскаватор выполнит всю работу, работая один.
7. Стороны треугольника, лежащего в основании пирамиды равны 13, 14, 15 см. Двугранные углы при основании пирамиды равны по 450. Найти боковую поверхность пирамиды.
Решение
Рис. 21
1. Проведем 
далее проведем OM 
AB, тогда SM AB по теореме о трех перпендикулярах, значит 
SMO = 450 - как линейный угол двугранного угла между гранями ASB и ABC (рис. 21).
2. Так как все двугранные углы при основании равны, то основание высоты пирамиды (точка O) попадет в центр вписанной в 
ABC (основание пирамиды) окружности.
3. Покажем, что, в этом случае, все апофемы боковых граней равны между собой и равны h. Сделаем это, рассмотрев две апофемы.
Проведем OD BC и соединим S с D, тогда SD BC по теореме о трех перпендикулярах, т. е. SD - апофема грани SBC.
SOM = SOD - как прямоугольные, имеющие равные катеты (OM = OD = r, SO - общий катет). Значит SM = SD = h.
4. Пусть S - площадь основания (треугольника), тогда 
а по формуле Герона 
где a, b, c - длины сторон треугольника, p - полупериметр.
5. Из SOM, 
6. Площадь боковой поверхности данной пирамиды равна:
Ответ: 
Вариант 6
1. Упростить: 
2. Решить неравенство: 
3. Решить уравнение: 
4. Решить уравнение: 
5. Доказать тождество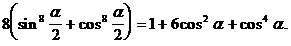 
6. Образующая усеченного конуса наклонена к его основанию, имеющему радиус R, под углом 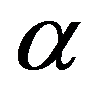; радиус другого основания равен r. Определить боковую поверхность усеченного конуса.
7. В круг радиуса r вписать прямоугольник с наибольшей площадью.
Решения
1. Упростить:
Решение
Множество значений переменных будет следующим: 
Ответ: 
, при
2. Решить неравенство:
Решение
Область допустимых значений переменной: 
Преобразуем неравенство и решим его методом промежутков, учитывая область допустимых значений переменной:
Разложим квадратный трехчлен 
на линейные множители. Он имеет корни: 
Тогда 
Неравенство примет вид: 
Рис. 22
Получим объединение промежутков (рис. 22):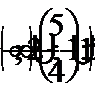 
Ответ: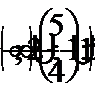
3. Решить уравнение: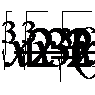
Решение
1-й способ
Поскольку все корни нечетной степени, то область допустимых значений переменной - множество всех действительных чисел, 
Возведем обе части уравнения в куб, получим:
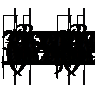
По условию 
тогда уравнение примет вид:
Последнее уравнение равносильно совокупности уравнений:
Проверка
При x = 1, получим: 
значит x = 1 является корнем уравнения.
