Ответ: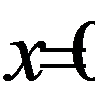 
.
5. Решить уравнение: 
Решение
Преобразуем уравнение:
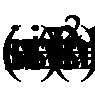
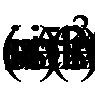
Для дальнейшего решения применим формулу преобразования суммы синусов в произведение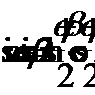 
а также формулу преобразования разности 
.
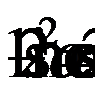Приходим к уравнению: 
Косинус функция четная, значит, 
, тогда уравнение примет вид: 
Получим совокупность двух уравнений: 
решая которые, находим:
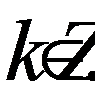
Ответ: 
6. Найти сторону тетраэдра, вписанного в шар радиуса R.
Решение
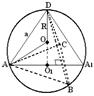
Рис. 9
1. Проведем высоту тетраэдра 
на основание ABC. Поскольку тетраэдр - правильная треугольная пирамида, тогда центр описанного шара будет находиться на высоте тетраэдра в точке O, DO = R - радиус описанного шара (см. рис. 9).
2. Проведем сечение шара плоскостью, проходящей через ребро тетраэдра AD и высоту перпендикулярно ребру BC. В результате, в сечении образуется круг радиуса R с центром в точке O, т. е. диаметральное сечение.
Точка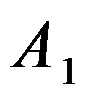 
лежит в плоскости основания и на окружности.
3. 
- равносторонний, R - радиус описанной около него окружности, тогда получим: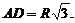 
Ответ: 
7. На кривой 
найдите точку, расстояние которой до прямой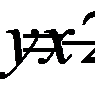 
будет наименьшим.
Решение
Пусть 
- точка, принадлежащая кривой 
, значит, ее координаты удовлетворяют уравнению кривой, т. е. при подстановке в уравнение обращают его в числовое равенство 
Пусть 
- точка, принадлежащая прямой 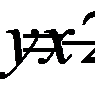, значит, 
.
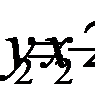Расстояние между этими двумя точками найдем по формуле:
Угловой коэффициент прямой (тангенс угла наклона к оси OX), проходящей через две точки и будет равен 
Угловой коэффициент прямой ,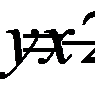 
Так как прямые 
и 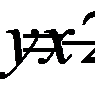перпендикулярны, тогда 
- по условию перпендикулярности прямых.
Отсюда следует, что 
Подставим в эту формулу значения 
и 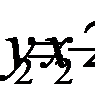получим:
Тогда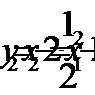 
Подставим значения 
и 
в формулу расстояния между двумя точками , получим:
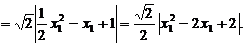
при условии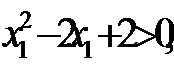 
но это неравенство выполняется при всех действительных значениях x, поскольку этот квадратный трехчлен имеет отрицательный дискриминант, значит, 
.
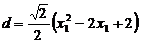Рассмотрим d как функцию от 
: 
и найдем ее наименьшее значение.
Производная этой функции равна: 
Найдем критические точки: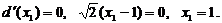 
Исследуем поведение функции в окрестности точки 1.
При 
, значит, функция на этом промежутке убывает.
При 
, значит, функция на этом промежутке возрастает.
В точке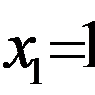 
функция имеет минимум. Следовательно, наименьшее расстояние будет при , 
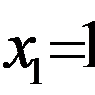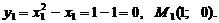
Ответ: 
Вариант 3
1. Упростить: 
2. Решить уравнение: 
3. Найти область определения функции:
4. Решить уравнение: 
.
5. Решить уравнение: 
6. Окружность проходит через вершины B, C, D трапеции ABCD и касается стороны AB в точке B. Найти длину диагонали BD, если длины оснований равны a и b.
7. Объем правильной треугольной призмы равен 16 дм3. Каковы должны быть основания и высота, чтобы площадь полной поверхности призмы была наименьшей?
Решения
1. Упростить: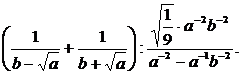 
Решение
Наложим ограничения на величины a и b: 
Ответ: 6b, при
2. Решить уравнение: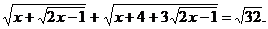 
Решение
Положим 
отсюда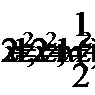 
получаем уравнение:
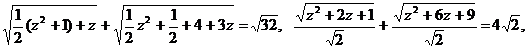
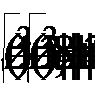
Мы получили линейное уравнение, содержащее модули. Найдем значения z, при которых каждый из модулей обращается в нуль. Это произойдет при z = -1 и 
Отметим эти точки на числовой прямой, получим три промежутка (рис. 10):
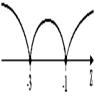
Рис. 10
Решим уравнение на каждом из этих промежутков.
1. При 
уравнение примет вид: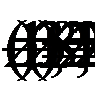 
- входит в промежуток и является корнем последнего линейного уравнения, содержащего модули.
2. При 
получим уравнение: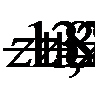 
- уравнение корней не имеет.
3. При 
получим уравнение: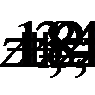 
- входит в промежуток 
и является корнем последнего уравнения.
Таким образом, в результате решения линейного уравнения получены два корня 
и 
Но один из них z = -6 не входит в область допустимых значений 
и является посторонним корнем. Остается один корень
Тогда получим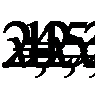 
Проверка
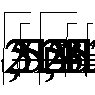
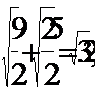
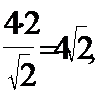
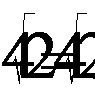
Ответ: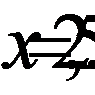 
3. Найти область определения функции: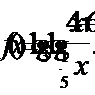 
Решение
Получим систему неравенств
Логарифмическая функция с основанием 
является убывающей, значит, получим систему неравенств:
Первые два неравенства решим методом промежутков с учетом третьего неравенства и найдем общие решения системы (рис. 11):
Рис. 11
Система имеет решения: 
Ответ:
4. Решить уравнение: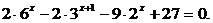 
Решение
Преобразуем уравнение:
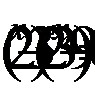Полученное уравнение равносильно совокупности уравнений:
Проверка
При 
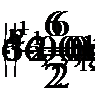- является корнем уравнения. При 
- является корнем уравнения.
Ответ: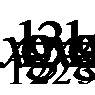 
5. Решить уравнение:
Решение
Преобразуем уравнение:
Получим совокупность уравнений:
Ответ: 
6. Окружность проходит через вершины B, C, D трапеции ABCD и касается стороны AB в точке B. Найти длину диагонали BD, если длины оснований равны a и b.
Решение
Рис. 12
1. AB - касательная к окружности в точке B, BC = a, AD = b, BD - диагональ.
Рассмотрим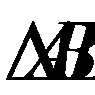 
и 
в них 
- как накрест лежащие при параллельных прямых BC и AD и секущей BD (см. рис. 12).
в 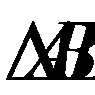образован касательной AB и хордой BD, значит, он измеряется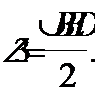 половиной дуги BED, 
- является вписанным и также измеряется половиной дуги, на которую опирается, т. е. половиной дуги BED, 
Значит, 
Отсюда следует, что 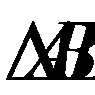подобен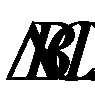 
2. Из подобия 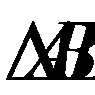и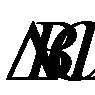 
следует, что
Ответ: 
7. Объем правильной треугольной призмы равен 16 дм3. Каковы должны быть основания и высота, чтобы площадь полной поверхности призмы была наименьшей?
Решение
Рис. 13
1. Объем правильной треугольной призмы равен произведению площади основания на высоту 
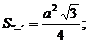
2. Площадь полной поверхности призмы равна:
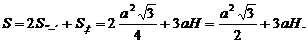
3. Выразим H из формулы объема: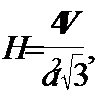 
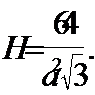
4. Подставим это значение в формулу площади полной поверхности:
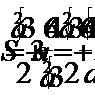
5. Рассмотрим площадь полной поверхности, как функцию от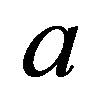 
и найдем ее наименьшее значение.
Найдем критические точки:
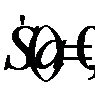
- критическая точка.
При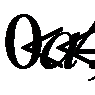 
значит функция убывает.
При 
значит функция возрастает.
В точке функция имеет минимум, а значит площадь боковой поверхности будет наименьшей. 
Ответ: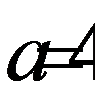 
дм, 
дм.
Вариант 4
1. Упростить: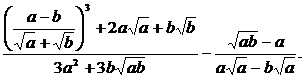 
2. Решить систему: 
3. Найти область определения функции:
4. Решить уравнение: 
5. Решить уравнение: 
6. В основании пирамиды лежит ромб. Высота пирамиды проходит через центр ромба. Боковые грани пирамиды образуют углы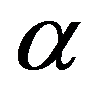 
и 
с диагоналями ромба. Найти угол наклона боковой грани к плоскости основания.
7. Найти высоту конуса максимального объема, который можно вписать в шар радиуса R.
Решения
1. Упростить: 
.
Решение
Это выражение имеет смысл при a > 0, b > 0 и 
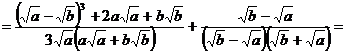
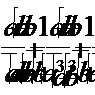
Ответ: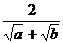 
, при a > 0, b > 0 и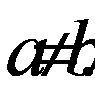 
2. Решить систему: 
Решение
Область допустимых значений переменных: 
Преобразуем систему уравнений:
Положим 
тогда получим систему уравнений:
Получим совокупность двух систем уравнений
(1) 
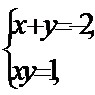и (2) 
(1) 
(2) 
Проверка
значит, 
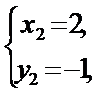являются решениями данной системы уравнений.
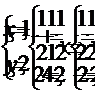значит, 
являются решениями данной системы уравнений.
значит, 
являются решениями данной системы уравнений.
Ответ: 
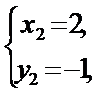
3. Найти область определения функции: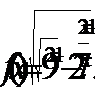 
Решение
Выражение, находящееся под знаком квадратного корня должно быть неотрицательным, значит, 
Поскольку, показательная функция принимает только положительные значения при всех значениях аргумента, тогда 
, следовательно, квадратный корень, в полученном неравенстве, будет определен при всех действительных значениях x.
В показателе степени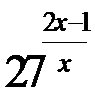 
находится дробь, знаменатель которой не должен быть равен нулю, значит, 
Получаем систему неравенств: 
Решим первое неравенство системы: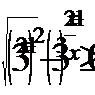 
Поскольку 
при всех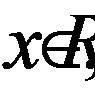 
тогда получим:
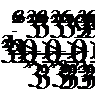
Но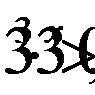 
приходим к неравенству: 
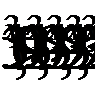
Так как показательная функция с основанием 3 > 1 является возрастающей, тогда находим 
Найдем решения системы неравенств 
используя изображение промежутков на числовых прямых (рис. 14):
