Графическое решение уравнения 6 страница

Составим систему уравнений:

Положим  и подставим в уравнения системы.

Во втором уравнении сократим на S, получим:

Решим второе уравнение и найдем x:

 не удовлетворяет условию задачи, поскольку отношение скоростей не может быть отрицательным, остается одно значение

Подставим это значение в первое уравнение и найдем :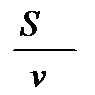

 

Ответ: время движения плота от A до B равно 4 ч.

4. Упростите

 

Решение

 

Выражение имеет смысл, если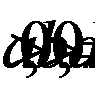

 

Ответ: 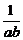, при .

 

5. Решить уравнение

 

Решение

 

Область допустимых значений

Воспользуемся формулой перехода от логарифмов одного основания к логарифмам другого

В левой части уравнения перейдем к логарифмам по основанию 2, получим:

Положим  получим

Проверка

 

 

 - является корнем уравнения.

 

 - является корнем уравнения.

Ответ:

 

6. В полукруг, радиус которого 1 дм вписана трапеция, так что одно ее основание - диаметр полукруга. Найти площадь трапеции, если периметр ее равен 5 дм.

 

Решение

 

Рис. 63

 

1. Сразу заметим, что в окружность может быть вписана только равнобедренная трапеция, значит AB = CD (см. рис. 63).

Рассмотрим 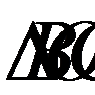 и проведем в нем высоту OM, которая также будет являться и высотой трапеции ABCD. В  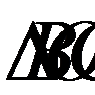BO = CO = R, поэтому он является равнобедренным, а следовательно, его высота OM будет являться и медианой, т. е. BM = MC.

Обозначим MC = x, тогда сторона BC = 2x.

2. В  проведем высоту CN, тогда CN = MO и также будет являться высотой трапеции.

Из 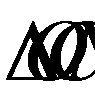 по теореме Пифагора  кроме того, отрезок ND будет равен разности ND = R - x, так как ON = MC = x - как противоположные стороны прямоугольника (параллелограмма).

3. Из  по теореме Пифагора

4. Периметр трапеции равен  подставляя значения получим:

Возведем обе части полученного равенства в квадрат, получим

5. Тогда BC = 1 дм, дм.

Площадь трапеции равна дм².

 

Ответ:

 

7. При каких значениях m корни уравнения 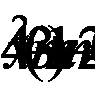 заключены в промежутке между -1 и 2?

 

Решение

 

Найдем условия, при которых функция  имеет корни  и 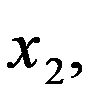 заключенные между числами  и

Во-первых, чтобы функция имела различные корни, дискриминант трехчлена должен быть положительным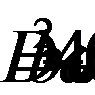

Поскольку первый коэффициент положительный, тогда ветви параболы - графика функции  должны быть направлены вверх (см. рис. 64).

 

Рис. 64

 

Во-вторых, абсцисса вершины параболы должна быть заключена на промежутке между p и q, т. е. .

В-третьих, значения функций в точках p и q должны быть положительны, так как точка p располагается левее точки , а точка q правее точки , а следовательно ветви параболы слева от  и справа от  расположены выше оси OX, т. е. значения

Эти три условия являются необходимыми и достаточными.

Таким образом, чтобы найти значения m, при которых корни трехчлена находились бы на заданном промежутке, необходимо решить систему неравенств:

Применим эти условия к данной задаче.

Найдем дискриминант

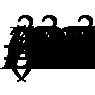
Найдем значения трехчлена в точках -1 и 2:

f(-1) = 4 + 3m + 1 + m - 2 = 4m + 3; f(2) = 16 - 6m - 2 - 2 - 2 = -6m + 10.

Найдем значение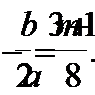  

Получим систему неравенств:

Находим общие решения систему с помощью числовых осей (см. рис. 65):

 

 

Рис. 65

 

Результатом будет промежуток

 

Ответ: при

 

Вариант 19

 

1. При каких значениях a наименьшее значение функции

 

 

равно –4.

2. Решить и исследовать неравенство: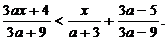

3. При всех значениях параметра a решить систему:

4. Найти все значения параметра a, для которых квадратные уравнения

имеют, по крайней мере, один общий корень.

5. При каких значениях p корни уравнения 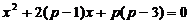 имеют разные знаки?

6. 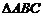 задан координатами вершин A(1; -1; 5), B(3; 4; 4), C(4; 6; 1). На плоскости xOy найти точку, проекцией которой на плоскости ABC служит центр описанной около  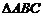окружности.

 

Решения

 

1. При каких значениях a наименьшее значение функции

 

 

равно –4.

Решение

 

Графиком этой функции является парабола, ветви которой направлены вверх (первый коэффициент 1 > 0) с вершиной в точке с координатами:

 

 

По условию:

 

 

 

Получили только одно значение , которое входит в промежуток

 

Проверим это значение.

 

При  функция примет вид: .

Ее вершина имеет координаты:

 

 

Условия задачи выполняются: 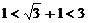, наименьшее значение равно –4.

 

Ответ: при .

 

2. Решить и исследовать неравенство: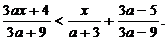

 

Решение

 

Преобразуем неравенство:

 

 

 

.

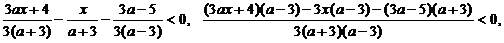
Полученное неравенство равносильно совокупности двух систем:

 

(1)                         и                 (2)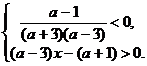

 

В свою очередь, каждая из этих систем равносильна совокупности еще двух систем.

Так, система (1), равносильна совокупности следующих систем:

(3)    и (4)

 

Решим эти системы (см. рис. 66):

(3)   

Рис. 66

В результате получаем, что при

Решим систему (4) (см. рис. 67):

 

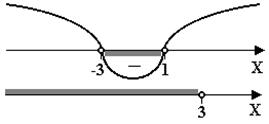(4)   

 

 

Рис. 67

В результате получаем, что при

Система (2) распадается на две совокупности систем (5) и (6) (см. рис. 68):

(2)

 

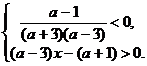
(5)  

 

 

Рис. 68

 

Эта система не имеет решений, поскольку первые два неравенства не имеют решений (см. рис. 69).

(6)  

 

 

Рис. 69

 

В результате решения этой системы получаем, что при  Объединяя решения всех систем, получаем окончательное решение заданного уравнения.

Ответ:

 

1. При

2. При .

 

3. При всех значениях параметра a решить систему:

 

Решение

 

Найдем главный и оба вспомогательных определителя системы:

 

 

.

1. Если , тогда система совместна и имеет единственное решение:

 

2. Если , тогда  система совместна и имеет бесконечное множество решений.

При a = 1, положим x = t, где t – любое действительное число, получим

.

При a = -1, получим

Ответ:

 

1. Если , тогда система совместна и имеет единственное решение:

2. Если , тогда система совместна и имеет бесконечное множество решений: при a = 1, 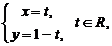 при a = -1,

 

4. Найти все значения параметра a, для которых квадратные уравнения

имеют, по крайней мере, один общий корень.

 

Решение

 

1. Прежде, рассмотрим те случаи значений параметра a, при которых первые коэффициенты каждого из уравнений обращаются в нуль.

В первом уравнении коэффициент при  равен нулю, при .

В этом случае, уравнения примут вид:  и .

Первое уравнение имеет один корень , а второе , вообще не имеет корней, значит мы можем с уверенностью можем положить, что  .

Во втором уравнении коэффициент при  равен нулю при .

В этом случае, уравнения примут вид: 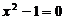 и .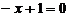

Первое уравнение имеет два корня: .

Второе уравнение имеет один корень: .

Таким образом, при  уравнения имеют один общий корень .

Для дальнейшего решения, положим, что  и .

2. При этих условиях, найдем значения a, при которых каждое из уравнений вообще имеет корни. В этом случае, дискриминанты каждого из уравнений должны быть неотрицательны.

Дискриминант первого уравнения равен: .

Дискриминант второго уравнения равен: .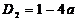

Чтобы оба уравнения имели действительные корни, должна выполняться система неравенств:

.

3. Теперь установим, когда уравнения будут иметь, по крайней мере, один общий корень. Для этого должно выполняться равенство:

Это уравнение, при  обращается в линейное и будет иметь один корень:

.

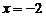Чтобы уравнение имело корни, его дискриминант должен быть неотрицательным: .

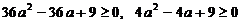. Это неравенство выполняется при всех действительных значениях a, т. е. при .

Обобщаем все рассмотренные случаи в виде смешанной системы:

Ответ: квадратные уравнения имеют, по крайней мере, один общий корень при .

 

5. При каких значениях p корни уравнения 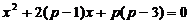 имеют разные знаки?

 

Решение

 

Чтобы уравнение имело корни разных знаков должны выполняться два условия:

1) уравнение должно иметь два различных действительных корня, для этого его дискриминант должен быть больше нуля:

;

2) по теореме Виета, произведение корней равно свободному члену, значит, если корни имеют разные знаки, то это произведение отрицательно: .

Получим систему неравенств (см. рис. 70):

 

 

 

Рис. 70

 

Решение системы неравенств является промежуток .

 

Ответ: при .

6.  задан координатами вершин A(1; -1; 5), B(3; 4; 4), C(4; 6; 1). На плоскости xOy найти точку, проекцией которой на плоскости ABC служит центр описанной около  окружности.

 

Решение

 

 

 

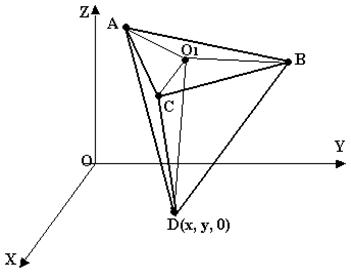
Рис. 71

 

Пусть D(x; y; 0) – искомая точка. По условию, ее проекцией на плоскость треугольника ABC, является точка  - центр описанной около этого треугольника окружности, значит DA = DC = DB (см. рис. 71), отсюда .

 

 

 

 

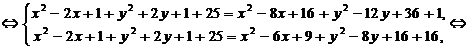
Ответ: (16; -5; 0).

 

7. Найти площадь равнобедренной трапеции, если высота равна h, а боковая сторона видна из центра описанной окружности под углом .

 

Решение

 

 

Рис. 72

 

1. Обозначим основания трапеции: b – меньшее основание, a – большее основание (a > b), тогда площадь трапеции равна:

2. Центры вписанной и описанной окружностей лежат на прямой, проходящей через середину оснований трапеции – точки M и N, значит  (см. рис. 72).

3. Из точки A проведены к вписанной окружности две касательные AN и AE, их отрезки равны, по теореме об отрезках касательных, выходящих из одной точки, значит,  По этой же причине

Получаем длину боковой стороны 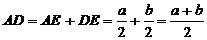, тогда площадь трапеции равна

4. Из трапеции ABCD находим, что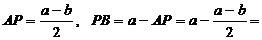  

, значит AD = PB.

5. Угол ABD – вписанный, опирающийся на дугу AD,  - центральный и тоже опирается на дугу AD,  - по условию, значит, .

6. Из  значит,

Ответ:

Вариант 20