Найдем корни трехчлена 
.
Разложим его на множители: 
.
Решим уравнение первой системы: 
.
Первая система примет вид
(1) 
Решим неравенства системы методом промежутков (см. рис. 46):
Рис. 46
Решением системы неравенств будет являться промежуток 
.
Ясно, что 
.
В результате решения первой системы получаем один корень: x = 1.
Решим вторую систему.
Решим квадратное уравнение системы:
.
Система примет вид:
(2) 
Рис. 47
В результате решения двух систем получаем два корня: 
(см. рис. 47).
Ответ: .
Графическое решение уравнения
Построим графики функций 
и 
. Абсциссы их точек пересечения и будут являться решениями заданного уравнения.
1. Для построения графика функции , построим параболу 
, а затем выполним "зеркальное" отражение в оси OX части параболы, лежащей ниже оси OX, иначе говоря, выполним симметрию нижней части параболы относительно оси OX.
Точки пересечения параболы с осью OX: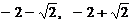 
.
Вершина параболы находится в точке с координатами:
.
2. Графиком функции является прямая, проходящая через точки:
.
3. Достаточно выполнить построения графиков справа от прямой 
, так как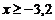 
. Выполним необходимые графические построения (см. рис. 48).
Рис. 48
Отсюда, также находим, что .
Ответ: .
3. Решить уравнение: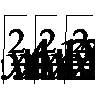 
Решение
Найдем область допустимых значений переменной. Каждый из трехчленов, находящихся под знаком квадратных корней имеют отрицательные дискриминанты, поэтому, при всех действительных значениях x они принимают положительные значения, т. е. областью допустимых значений является множество всех действительных чисел, 
.
Положим 
тогда 
.
Уравнение примет вид 
.
Область допустимых значений переменной z:
, или 
.
Возведем обе части уравнения в квадрат, получим:
.
Возведем еще раз в квадрат обе части уравнения, получим:
. 
не удовлетворяет условию 
и является посторонним корнем. Остается один корень, 
.
Выполним обратную подстановку 
.
Ответ: .
4. Решить уравнение: 
Решение
Преобразуем уравнение 
. Разделим обе части уравнения на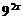 
, зная, что 
.
Получим следующее уравнение:
.
Положим 
. Получим квадратное уравнение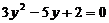 
.
.
Проверка
- корень уравнения.
- корень уравнения.
Ответ: 
.
5. Решить уравнение: 
Решение
Область допустимых значений переменной определим, учитывая, что знаменатели дробей не должны равняться нулю:
Преобразуем уравнение:
.
Получим совокупность двух уравнений:
(
1) 
.
(2) 
- уравнение не имеет решений.
Установим, входят ли найденные решения в область допустимых значений:
Первое и третье неравенства выполняются, а из второго неравенства следует, необходимо исключить из полученного множества решений те значения, при которых n = 2m.
. Другими словами, n не должно принимать четные значения, следовательно, n может принимать только нечетные значения 
.
Ответ: 
.
6. Два велосипедиста выехали одновременно из одного пункта в одном направлении. Первый из них ехал со скоростью 15 км/ч, а второй - со скоростью 12км/ч. Спустя полчаса из того же пункта в том же направлении выехал третий велосипедист, который через некоторое время догнал второго, а еще через 1 час 30 мин. догнал и первого. Найти скорость третьего велосипедиста.
Решение
Пусть
x км/ч - скорость третьего велосипедиста,
y км/ч - его время движения до встречи со 2-м велосипедистом,
(y + 3/2) ч - его время движения до встречи с 1-м велосипедистом,
(y + 0,5) ч - время движения 2-го велосипедиста до встречи с 3-м,
(y + 3/2 + 0,5) = (y + 2)ч - время движения 1-го велосипедиста до встречи с 3-м,
xy км - путь, пройденный 3-м велосипедистом до встречи со 2-м,
12(y + 0,5) км - путь, пройденный 2-м велосипедистом до встречи с 3-м.
Составим уравнение
xy = 12(y + 0,5)
x(y + 3/2) км - путь, пройденный 3-м велосипедистом до встречи с 1-м,
15(y + 2) км - путь, пройденный 1-м велосипедистом до встречи с 3-м.
Составим уравнение
x(y + 3/2) = 15(y + 2)
Составим систему уравнений и решим ее
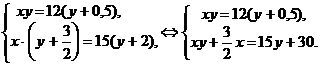
Из первого уравнения подставим во второе значение произведения xy, получим: 
.
Подставим полученное значение y в первое уравнение:
.
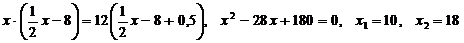Ясно, что первый корень уравнения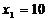 
не удовлетворяет условию задачи, так как скорость у 3-го велосипедиста должна быть больше, чем у 2-го и 1-го.
Ответ: 18 км/ч - скорость 3-го велосипедиста.
7. Найти радиус основания r и высоту h прямого кругового конуса, вписанного в шар радиуса R так, чтобы его объем был наибольшим.
Решение
Рис. 49
1. Обозначим OO1 = x, тогда высота конуса h = R + x (см. рис. 49).
2. Из 
.
3. Объем конуса равен 
.
4. Рассмотрим объем конуса, как функцию от x,
, где 0 < x < R.
Найдем производную этой функции:
.
Найдем критические точки, V'(x) = 0.
.
не входит в промежуток 
.
Остается одна критическая точка 
. Исследуем поведение функции в окрестности этой точки.
При 
- функция возрастает.
При 
- функция убывает.
Значит, в точке функция имеет максимум, т. е. конус имеет максимальный объем, 
.
Найдем радиус основания конуса. Из 
по теореме Пифагора, имеем:
.
Ответ: 
.
Вариант 13
1. Упростить выражение:
2. Решить систему: 
3. Решить неравенство: 
4. Решить уравнение: 
5. Решить уравнение: 
6. В равнобочную трапецию, длины оснований которой a и b (a > b), можно вписать окружность. Найти расстояние между центрами вписанной и описанной окружностей.
7. Какую наименьшую площадь может иметь треугольник, на гипотенузе которого лежит точка M(2; 1), а катеты - отрезки координатных осей.
Решения
1. Упростить выражение:
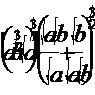
Решение
Выражение имеет смысл, если 
.
.
Ответ: 
, при .
2. Решить систему:
Решение
Область допустимых значений 
.
Из первого уравнения находим 
, отсюда получаем совокупность уравнений, что 
и 
.
Получим совокупность двух систем уравнений:
(1) 
и (2) 
Преобразуем второе уравнение каждой системы:
.
Системы уравнений примут вид:
(1) 
и (2) 
Решим первую систему. Выразим из первого уравнения y и подставим во второе уравнение, получим 
.
Это уравнение, в свою очередь, равносильно совокупности двух систем:
(1') 
.
(2') 
.
Решим вторую систему уравнений (2) 
Выразим из первого уравнения y и подставим во второе уравнение 
.
Получим совокупность двух смешанных систем:
(3') 
Эта система не имеет решений.
(4') 
Эта система также не имеет решений.
В результате получаем два решения 
Эти решения входят в область допустимых значений.
Проверка
Эти значения удовлетворяют системе.
Эти значения также удовлетворяют системе уравнений.
Ответ:
3. Решить неравенство: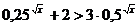 
.
Решение
Область допустимых значений: 
.
Преобразуем неравенство: 
.
Положим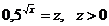 
. Получим систему неравенств:
Решим систему методом промежутков (см. рис. 50).
Рис. 50
Получаем 
и 
.
Выполним обратную подстановку и найдем значения x.
Получим совокупность неравенств: 
Показательная функция с основанием 0,5 < 1 является убывающей, тогда, из первого неравенства получим: 
.
Из второго неравенства: 
. Последнее неравенство, очевидно, не имеет решений.
Ответ: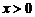 
.
4. Решить уравнение:
Решение
Найдем область допустимых значений, учитывая, что переменная находится в основании логарифма, а также в знаменателе дроби и под знаком логарифма:
.
Преобразуем уравнение:
- не входит в область допустимых значений и не является корнем уравнения.
Ответ: 
.
5. Решить уравнение:
Решение
Преобразуем уравнение, используя формулу 
, получаем:
Положим 
, получим квадратное уравнение
.
Ответ: 
; 
.
6. В равнобочную трапецию, длины оснований которой a и b (a > b), можно вписать окружность. Найти расстояние между центрами вписанной и описанной окружностей.
Решение
Рис. 51
1. Необходимо найти расстояние OO1. Для этого надо знать длины отрезков ON и NO1, ON = r - радиус вписанной окружности. Отрезок O1N обозначим x.
Чтобы найти x, необходимо найти радиус описанной окружности R и тогда из 
можно найти x, а затем и расстояние OO1 (см. рис. 51).
2. Понятно, что центры вписанной и описанной окружностей лежат на прямой, проходящей через середины оснований - точки M и N, значит, 
.
3. Из точки A проведены к вписанной окружности две касательные AN и AE, их отрезки равны, по теореме об отрезках касательных, выходящих из одной точки, значит 
. По этой же причине 
.
Получаем длину боковой стороны 
.
Отрезок 
.
Из 
по теореме Пифагора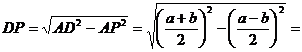 
.
4. Из найдем 
из 
по теореме Пифагора найдем BD. Но, прежде, найдем BP, 
,
.
5. Применим теорему синусов к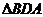 
, который является вписанным в окружность радиуса R.
.
6. Из по теореме Пифагора 
.
7. Окончательно находим: 
,
.
Ответ: 
.
7. Какую наименьшую площадь может иметь треугольник, на гипотенузе которого лежит точка M(2; 1), а катеты - отрезки координатных осей.
Решение
Рис. 52
1. Пусть AOB - заданный треугольник, у которого катет OA лежит на оси OX, катет OB лежит на ординате OY, AB - гипотенуза, на которой лежит точка M с координатами (2; 1), M(2; 1) (см. рис. 52).
Обозначим длину катета OA = a, тогда координаты точки A будут A(a; 0).
2. Составим уравнение гипотенузы AB, как уравнение прямой, проходящей через две точки M(2; 1) и A(a; 0):
.
3. Эта прямая проходит через точку B с координатами (0; b). Подставим координаты этой точки в уравнение прямой, и найдем значение координаты b по Y.
.
4. Но координата точки B по оси OY равна длине катета OB, значит, 
.
Тогда, площадь треугольника будет равна 
.
5. Рассмотрим площадь треугольника, как функцию от a и исследуем её:
.
Найдем производную этой функции и критические точки:
.
Критические точки: a = 0, a = 2, a = 4.
Две первые точки a = 0, a = 2 не входят в область определения функции.
Исследуем поведение функции в окрестности точки a = 4.
При 
, значит функция убывает.
При 
, значит функция возрастает.
