Графическое решение уравнения 5 страница

Рис. 58

Результатом решения будет объединение промежутков: (см. рис. 58).

Ответ: .

4. Решить уравнение:

Решение

Область допустимых значений: .

Преобразуем уравнение:

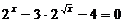. Так как , тогда получим: . Положим , получим квадратное уравнение:

. - не удовлетворяет условию и не является корнем уравнения. Остается один корень, y = 4.

Ответ: .

5. Решить уравнение:

Решение

Для преобразования уравнения применим тригонометрическую формулу:

, в которой положим , тогда получим

Подставляя это значение в уравнение будем иметь:

Применим формулу преобразования суммы косинусов в произведение, получим уравнение:

Каждый из множителей в левой части уравнения может равняться нулю, получим совокупность двух уравнений:

Ответ: , .

6. Найти радиус шара вписанного в тетраэдр со стороной a.

Решение

Рис. 59

1. Пусть ABCD - тетраэдр, DO - его высота, O₁K - радиус вписанного шара, (см. рис. 59).

2. AO является радиусом вписанной в основание окружности, поэтому . Из прямоугольного треугольника ADO, высота DO, по теореме Пифагора будет равна: .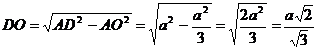

3. DO₁ = DO - r. подобен , как прямоугольные, имеющие общий острый угол. Из их подобия следует, что

Ответ: .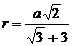

7. На параболе найти точку, расстояние от которой до точки M(9; 3) будет наименьшим.

Решение

Пусть A(x; y) - точка, принадлежащая параболе, является искомой, т. е. расстояние между точкамиA и M будет наименьшим.

Расстояние между этими точками определяется формулой: .

Так как точка A принадлежит параболе, тогда .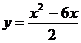

Подставим это значение в формулу расстояния, получим:

Рассмотрим это расстояние, как функцию от x и найдем ее наименьшее значение, причем рассматривать будем функцию на множестве действительных чисел, при которых .

Для этого, найдем производную и критические точки:

Поскольку те точки, при которых знаменатель равен нулю исключаются из рассмотрения, так как они не входят в область определения функции, то критическими будут точки, при которых производная будет равна нулю (см. рис. 60):

Рис. 60

При , значит, функция, на этом промежутке, убывает.

При , значит, функция, на этом промежутке, возрастает.

При , значит, функция, на этом промежутке, убывает.

При , значит, функция, на этом промежутке, возрастает.

В точках x = 0 и x = 7 функция принимает минимальные значения.

Наименьшее значение функция принимает при x = 7.

Координаты точки: x = 7, y = 3,5; A(7; 3,5).

Ответ: .

Вариант 17

1. Три числа составляют геометрическую прогрессию. Если от третьего отнять 4, то числа составят арифметическую прогрессию. Если же от второго и третьего числа полученной арифметической прогрессии отнять 1, то снова получится геометрическая прогрессия. Найти эти числа.

2. Решить уравнение:

3. Пешеход и велосипедист отправляются одновременно из пункта A в пункт B. В пункте B велосипедист поворачивает обратно и встречает пешехода через 20 минут после начала движения. Не останавливаясь, велосипедист доезжает до пункта A, поворачивает обратно и догоняет пешехода через 10 минут после первой встречи. За какое время пешеход пройдет путь от A до B?

4. Упростить выражение:

5. Решить уравнение: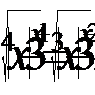

6. К окружности с центром в точке O проведены касательные AB и AC. M - точка пересечения луча OA с окружностью, DE - отрезок касательной, проведенной через точку M, заключенный между AB и AC. Определить |DE|, если |AO| = 39 см и радиус окружности равен 15 см.

7. При каких значениях p оба корня квадратного трехчлена

отрицательны?

Решения

Решение

1. Пусть a, b, c - искомые числа. Они составляют геометрическую прогрессию, значит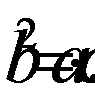

2. Если от третьего отнять 4, то числа образуют арифметическую прогрессию, т. е. числа a, b и c - 4. Следовательно,

3. Если от второго и третьего числа, полученной арифметической прогрессии отнять 1, то получим следующие числа: a, b - 1, c - 5. Они образуют геометрическую прогрессию, значит

Получим систему из трех уравнений:

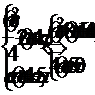
Из второго уравнения выразим a и подставим в первое уравнение.

Таким образом, получаем два результата:

1) 0; 0; 4 и 2)

Первый результат не удовлетворяет условию задачи, так как числа 0, -1, - 1 не образуют геометрическую прогрессию.

Удовлетворять условию задачи будет вторая группа чисел

Ответ:

2. Решить уравнение:

Решение

Преобразуем уравнения, используя формулы приведения и формулы преобразования произведения синусов и косинусов в сумму:

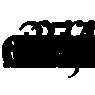
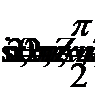
Ответ:

Решение

Рис. 60

Пусть t ч - время движения пешехода от A до B, S км - расстояние от A до B,

км/ч - скорость пешехода, км/ч - скорость велосипедиста.

км - путь, пройденный пешеходом до первой встречи,

км - путь, пройденный велосипедистом до первой встречи (см. рис. 60).

Получим уравнение

км - путь, пройденный пешеходом от первой встречи до второй встречи,

км - путь, пройденный велосипедистом от первой встречи до второй.

Получим уравнение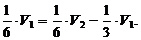

Приходим к системе уравнений

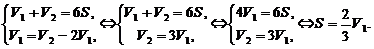
Но тогда 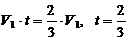ч или t = 40 мин.

Ответ: 40 мин.

4. Упростить выражение:

Решение

Ответ: , при .

5. Решить уравнение: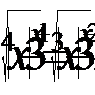

Решение

Преобразуем уравнение, при этом рассмотрим три случая.

1-й случай, когда , тогда получим уравнение:

- входит в промежуток и является корнем уравнения.

2-й случай, когда тогда получим уравнение:

- не входит в промежуток и не является корнем уравнения.

3-й случай, когда тогда получим:

- является корнем уравнения.

Ответ:

Решение

Рис. 61

1. Применим теорему: "Квадрат отрезка касательной равен произведению секущей на ее внешний отрезок". В качестве касательной рассмотрим AB, секущей является AK. По этой теореме

(см) (см. рис. 61).

2. Рассмотрим и 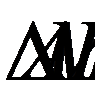они подобны, как прямоугольные, имеющие общий острый угол OAB. Из подобия этих треугольников следует:

(см).

3. Треугольники AMD и AME равны, как прямоугольные, имеющие общий катет AM и равные острые углы OAB и OAC, значит (см).

Ответ:

7. При каких значениях p оба корня квадратного трехчлена

отрицательны?

Решение

Во-первых, определим, при каких значениях p трехчлен имеет корни.

Для этого его дискриминант должен быть неотрицательным:

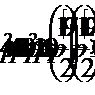
Если оба корня трехчлена отрицательны, тогда его свободный член, равный по теореме Виета произведению корней, должен быть положительным, а сумма корней, равная второму коэффициенту, взятому с противоположным знаком, должна быть отрицательной.

Получим систему неравенств:

Учитывая, множество значений p, при которых трехчлен имеет корни, получаем множество (см. рис. 62):

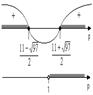
Рис. 62

Ответ:

Вариант 18

1. Три числа образуют геометрическую прогрессию. Если второе число увеличить на 2, то прогрессия станет арифметической, а если после этого, увеличить последнее число на 9, то прогрессия снова станет геометрической. Найти числа.

2. Решить уравнение:

3. Пристань A находится выше течению реки, чем пристань B. Из A в B одновременно навстречу друг другу начинают движение плот и моторная лодка. Достигнув пристани A моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он прошел расстояния между A и B. Найти время движения плота от A до B, если моторная лодка проплывает путь из B в A и обратно за 3 ч.

4. Упростите

5. Решить уравнение

6. В полукруг, радиус которого 1 дм вписана трапеция, так что одно ее основание - диаметр полукруга. Найти площадь трапеции, если периметр ее равен 5 дм.

7. При каких значениях m корни уравнения 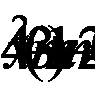заключены в промежутке между -1 и 2?

Решения

Решение

Пусть a, b, c - искомые числа.

Они образуют геометрическую прогрессию, значит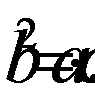

После увеличения второго числа на 2, числа станут такими: a, b + 2, c. По условию, они будут образовывать арифметическую прогрессию, значит

После увеличения третьего числа на 9, числа станут: a, b + 2, c + 9.

По условию, они снова будут образовывать геометрическую прогрессию, значит

Получим систему, состоящую из трех уравнений, решая которую найдем искомые числа.

Решим полученную систему. Для этого из второго уравнения значения b + 2 подставим в третье уравнение, а затем, выразив из него b, подставим в первое уравнение, получим:

Из третьего уравнения, значения подставим в первое уравнение, получим:

Полученное значение c подставим в третье уравнение:

Таким образом, получаем две группы чисел и

Проверим каждую из двух троек чисел.

Первоначально они должны образовывать геометрическую прогрессию, значит: - первое условие выполняется.

Затем, ко второму числу прибавили 2 и получили арифметическую прогрессию, проверим и это.

Второе число станет:

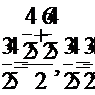- второе условие выполняется.

После увеличения третьего числа на 9, оно станет равным

Числа должны снова образовывать геометрическую прогрессию, проверим это.

- третье условие выполняется.

Значит, числа удовлетворяют условию задачи.

Проверим вторую тройку чисел

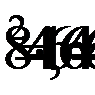- числа образуют геометрическую прогрессию, первое условие выполняется.

После увеличения второго на 2, они станут равными

- числа образуют арифметическую прогрессию, второе условие выполняется.

После увеличения третьего числа на 9, получим

- числа снова образуют геометрическую прогрессию.

Значит и эта тройка чисел удовлетворяет условию.

Ответ: ,

2. Решить уравнение:

Решение

В правой части уравнения разложим разность квадратов на множители, а затем применим формулы преобразования суммы и разности косинусов в произведение:

Левую часть уравнения преобразуем, используя формулы преобразования суммы синусов в произведение:

Уравнение примет вид:

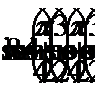
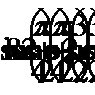
Ответ:

Решение

Пусть S - расстояние между пунктами A и B, u - собственная скорость лодки (скорость лодки в стоячей воде), v - скорость плота (скорость течения реки), тогда 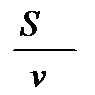- время движения плота от A до B.