В точке a = 4 функция S(a), т. е. площадь, будет иметь наименьшее значение, которое равно 
.
Ответ: S = 4 кв. ед.
Вариант 14
1. Упростить: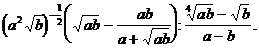 
2. Решить уравнение: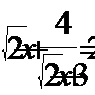 
3. Решить неравенство: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Найти площадь треугольника, если длины двух его сторон равны 1 см. и 
см., а длина медианы третьей стороны равна 2 см.
7. Группа студентов решила купить магнитофон ценой от 170 тыс. руб. до 195 тыс. руб. Однако, в последний момент двое отказались участвовать в покупке, поэтому каждому из остальных пришлось внести на 1 тыс. руб. больше. Сколько стоил магнитофон?
Решения
1. Упростить: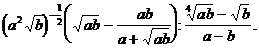
Решение
Область допустимых значений переменных a и b: 
.
.
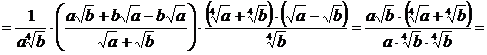
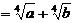Ответ: 
, при .
2. Решить уравнение: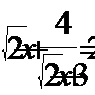
Решение
Положим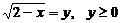 
, получим:
,
- не удовлетворяет условию 
и является посторонним корнем.
Получим уравнение: 
, которое равносильно системе:
.
Ответ: 
.
3. Решить неравенство:
Решение
Область допустимых значений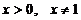 
, так x находится не только под знаком логарифма, но и в основании логарифма.
Перейдем, в уравнении, к логарифмам по основанию 3, получим:
.
Решим полученное неравенство методом промежутков. Для этого разложим трехчлен на множители:
(см. рис. 53),
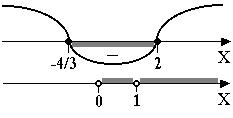
Рис. 53
В результате, получаем множество из объединения промежутков:
.
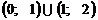Ответ: .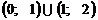
4. Решить уравнение:
Решение
Область допустимых значений: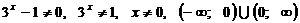 
.
Преобразуем уравнение
.
Положим 
, получим уравнение:
.
Ответ: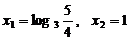 
.
5. Решить уравнение:
Решение
Для преобразования уравнения применим следующие тригонометрические формулы:
, откуда 
;
а также 
.
Получим уравнение: 
.
Полученное уравнение равносильно совокупности уравнений:
Ответ: 
.
6. Найти площадь треугольника, если длины двух его сторон равны 1 см. и см., а длина медианы третьей стороны равна 2 см.
Решение
1-й способ
Длина медианы треугольника, проведенной к стороне a определяется по формуле: 
, где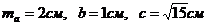 
.
Возведем обе части этого равенства в квадрат, получим:
.
Подставляя числовые значения, находим: 
см.
Площадь найдем по формуле Герона 
, где p - полупериметр, 
a, b, c - длины сторон треугольника.
.
см2.
Ответ: 
.
2-й способ
Рис. 54
1. Пусть DM = x (см. рис. 55).
2. Из 
по теореме Пифагора 
, из 
по теореме Пифагора 
, из 
.
3. Получим систему уравнений, из которой найдем x, причем заметим, AM=MC.
Из второго уравнения выразим x и подставим в первое уравнение, получим:
.
4. Найдем высоту треугольника
.
5. Найдем площадь 
см2.
Ответ: .
7. Группа студентов решила купить магнитофон ценой от 170 тыс. руб. до 195 тыс. руб. Однако, в последний момент двое отказались участвовать в покупке, поэтому каждому из остальных пришлось внести на 1 тыс. руб. больше. Сколько стоил магнитофон?
Решение
Пусть x тыс. руб. - первоначальный взнос каждого студента, y - число студентов в группе, тогда 170 < xy < 195.
(y - 2) - число студентов, которые участвовали в покупке, (x + 1) тыс. руб. - по столько пришлось уплатить каждому, чтобы купить магнитофон.
Получим уравнение: 
.
Из уравнения находим x: 
.
Подставим это значение в двойное неравенство: 170 < xy < 195, получим:
.
Это двойное неравенство равносильно системе неравенств:
В результате решения получаем: 
.
Первое двойное неравенство не удовлетворяет условию задачи, так как состоит из множества отрицательных чисел.
Таким образом, решениями системы будет множество: 
.
Так как y - натуральное число, то последней системе неравенств удовлетворяют два числа: 19 и 20. Все условия задачи выполняются лишь при y = 20, x = 9, поэтому xy = 180.
Ответ: 180 тыс. руб.
Вариант 15
1. Упростить: 
2. Решить неравенство: 
3. Решить уравнение: 
4. Решить уравнение: 
5. Доказать тождество: 
6. Угол при вершине сечения прямого кругового конуса равен 
, а его высота равна h. Определить радиус шара, вписанный в конус.
7. Найти размеры конической палатки данной вместимости, требующей наименьшее количество материала.
Решения
1. Упростить:
Решение
Выражение имеет смысл, если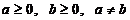 
.
.
Ответ: 3, при .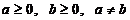
2. Решить неравенство:
Решение
Найдем область допустимых значений. Трехчлены, находящиеся в знаменателях дробей не должны равняться нулю:
Преобразуем неравенство:
.
Это неравенство решим методом промежутков. Для этого определим те значения переменных, при которых каждый из линейных множителей обращаются в нуль, независимо от того, находится ли он в числителе или в знаменателе.
Эти значения следующие: 
.
Точки изображаем на числовой прямой и проводим с правого верхнего угла кривую через первую точку вниз, через вторую вверх и т. д. (см. рис. 55).
|
Рис. 55
При тех значениях x, где кривая находится выше оси OX, данная дробь положительна. Окончательно получаем.
Ответ: 
.
3. Решить уравнение:
Решение
1-й способ
Найдем область допустимых значений:
.
Преобразуем уравнение:
.
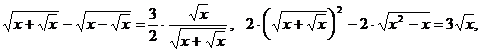
Возведем обе части полученного уравнения в квадрат, но перед этим потребуем, чтобы 
. Откуда, учитывая область допустимых значений, находим: 
, что и подавно выполняется, так как область допустимых значений 
.
На этом множестве, возведем обе части уравнения 
в квадрат, получим: 
.
Это значение входит в область допустимых значений и является корнем уравнения.
Ответ: 
.
2-й способ
.
Положим 
тогда получим
, вычитая из первого уравнения второе, находим:
.
Подставим в первоначальное уравнение, значения u и v, а также 
, приходим к уравнению:
.
Отсюда находим, что 
,
, но это невозможно, так как область допустимых значений переменной x, .
, 
.
Ответ: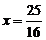 
.
4. Решить уравнение:
Решение
Найдем область допустимых значений:
.
Преобразуем уравнение:
. Это значение входит в область допустимых значений и является корнем уравнения.
Проверка
При 
, 
.
Значит - корень уравнения.
Ответ: .
5. Доказать тождество:
Доказательство
Преобразуем левую часть тождества:
. Тождество доказано.
6. Угол при вершине сечения прямого кругового конуса равен , а его высота равна h. Определить радиус шара, вписанный в конус.
Решение
Рис. 56
Пусть сечение конуса является осевым. Тогда в сечении будет равнобедренный треугольник ASB (AS = BS). Высота конуса будет являться медианой и биссектрисой, значит 
- прямоугольный, в нем OS - гипотенуза, 
, где h - высота конуса, r - радиус вписанного шара (см. рис. 56).
Из 
.
Ответ: 
.
7. Найти размеры конической палатки данной вместимости, требующей наименьшее количество материала.
Решение
1. Пусть V - вместимость палатки, т. е. ее объем. Пусть h - высота конической палатки, R - радиус основания, l - образующая конуса. Тогда объем конической палатки будет равен 
, а площадь ее боковой поверхности будет равна 
тогда 
.
2. Выразим из формулы объема радиус R и подставим его значение в формулу площади боковой поверхности:
.
3. Рассмотрим площадь боковой поверхности, как функцию от h, для h > 0 и найдем ее наименьшее значение на промежутке h > 0.
Найдем производную и критические точки:
.
Критические точки: 
- единственная критическая точка.
При 
, значит функция убывает.
При 
, значит функция возрастает.
В точке 
функция Sб, т. е. площадь боковой поверхности имеет наименьшее значение, а значит, материала на палатку пойдет меньше.
Радиус основания, в этом случае, будет равен:
.
Ответ: , 
.
Вариант 16
1. Упростить: 
2. Решить уравнение: 
3. Найти область определения функции:
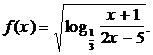
4. Решить уравнение: 
5. Решить уравнение: 
6. Найти радиус шара вписанного в тетраэдр со стороной a.
7. На параболе 
найти точку, расстояние от которой до точки M(9; 3) будет наименьшим.
Решения
1. Упростить:
Решение
Выражение имеет смысл, если 
.
2. Решить уравнение:
Решение
Линейные функции, находящиеся под знаками модулей, меняют знак при переходе через точки, обращающие их в нуль, т. в точках x = 2 и x = 5 (см. рис. 57).
Рис. 57
Рассмотрим данное уравнение на каждом из полученных трех промежутков.
1. При 
уравнение примет вид: 
.
Решая его, находим: 
, значит, x = -5 является корнем уравнения.
2. При 
уравнение примет вид: 
.
Решая его, находим: 
и не является корнем уравнения.
3. При 
, уравнение примет вид: 
.
Решая его, находим: 
и не является корнем уравнения.
Ответ: 
.
3. Найти область определения функции:
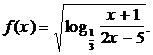
Решение
Выражение, находящееся под знаком квадратного корня должно быть неотрицательным, значит 
. Выражение, находящееся под знаком логарифма должно быть положительным: 
.
Получим систему неравенств:
При переходе от логарифмов к выражениям, находящимся под знаками логарифмов, было использовано свойство логарифмической функции с основанием 
, которая является убывающей, а значит, большему значению логарифма соответствует меньшее значение функции, и наоборот, меньшему значению аргумента соответствует большее значение функции.
