Решение
1. Прежде установим, при каких значениях a уравнение будет иметь действительные корни. Для этого дискриминант должен быть неотрицательным, т. е.

Найдем корни трехчлена 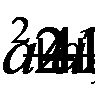 имя являются
имя являются 
Разложим трехчлен на множители

Решим методом интервалов неравенство 
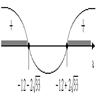
Рис. 37
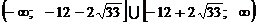 (см. рис. 37).
(см. рис. 37).
2. Преобразуем уравнение к приведенному, получим 
По теореме Виета для этого уравнения находим: 
С другой стороны, преобразуем заданное выражение


Подставляем значения вместо суммы и произведения корней, полученных из теоремы Виета, получим

Ответ:  при
при 
3. Решить неравенство: 
Решение
Это неравенство можно записать в виде двойного неравенства
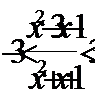
или в виде систему неравенств


Так как трехчлен  при всех действительных значениях переменной
при всех действительных значениях переменной 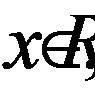 ибо его дискриминант отрицателен
ибо его дискриминант отрицателен  а первый коэффициент больше нуля
а первый коэффициент больше нуля  тогда, умножив каждое из уравнений системы на положительное при всех x выражение, т. е. на
тогда, умножив каждое из уравнений системы на положительное при всех x выражение, т. е. на  , получим равносильную систему:
, получим равносильную систему:

Неравенство 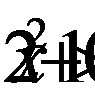 также выполняется при всех
также выполняется при всех 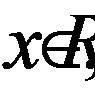 значит система равносильна неравенству
значит система равносильна неравенству  которое решим методом интервалов (см. рис. 38),
которое решим методом интервалов (см. рис. 38),

Рис. 38
получим 
Ответ: 
4. Решить уравнение: 
Решение
Область допустимых значений 
Преобразуем уравнение. Для этого перейдем к логарифмам по основанию 2, для этого используем формулу перехода от логарифмов одного основания к логарифмам другого 
Уравнение примет вид
 отсюда находим
отсюда находим  Это значение входит в область допустимых значений.
Это значение входит в область допустимых значений.
Ответ: 
5. Решить уравнение: 
Решение
Область допустимых значений переменной 
Преобразуем уравнение




Ответ: 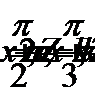
6. Из двух городов выехали одновременно навстречу друг другу два автомобиля. Первый за 3 ч прошел 0,08 всего расстояния между городами, а второй за 2,5 ч. 7/120 этого расстояния. Найдите (в км/ч) скорость второго автомобиля, если до места встречи первый прошел 800 км.
Решение

Рис. 39
 км/ч - скорость первого автомобиля (см. рис. 39),
км/ч - скорость первого автомобиля (см. рис. 39),
 км/ч - скорость второго автомобиля,
км/ч - скорость второго автомобиля,
S км - весь путь.
По условию:

 ч - время движения первого автомобиля до встречи.
ч - время движения первого автомобиля до встречи.
 ч - время движения второго автомобиля до встречи.
ч - время движения второго автомобиля до встречи.
Составим уравнение
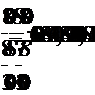 (км).
(км).
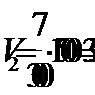 (км/ч).
(км/ч).
Ответ: 35 км/ч.
7. Боковая грань правильной треугольной пирамиды образует с плоскостью основания угол 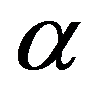 , сумма длин высоты пирамиды и радиуса окружности, вписанной в основание пирамиды равна a. Найти объем пирамиды.
, сумма длин высоты пирамиды и радиуса окружности, вписанной в основание пирамиды равна a. Найти объем пирамиды.
Решение
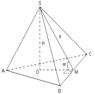
Рис. 40
1. Проведем  SO - высота пирамиды, SO = H (см. рис. 40).
SO - высота пирамиды, SO = H (см. рис. 40).
O - центр вписанной в основание (треугольник) окружности, так как пирамида правильная, да и все боковые грани наклонены под одним углом к плоскости основания.
2. Проведем  и соединим S и M, тогда
и соединим S и M, тогда 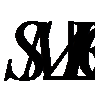 по теореме о трех перпендикулярах, а значит
по теореме о трех перпендикулярах, а значит  - линейный угол двугранного угла, образованного боковой гранью и плоскостью основания, а следовательно
- линейный угол двугранного угла, образованного боковой гранью и плоскостью основания, а следовательно 
3. Из 
 и по условию H + r = a, получим систему уравнений:
и по условию H + r = a, получим систему уравнений:
 отсюда находим
отсюда находим 

4. 
5. 
Ответ: 
Вариант 11
1. Упростить выражение: 
2. Решить уравнение: 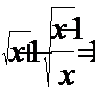
3. Найти область определения функции: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Отношение оснований равнобедренной трапеции равно m. Найти отношение радиусов окружностей, описанной около трапеции и вписанной в нее.
7. Определить размеры открытого бассейна объемом 32 см3 с квадратным дном, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение
1. Упростить выражение: 
Решение
Найдем значения a, при которых выражение имеет смысл:

Итак, выражение имеет смысл, если a > 1.
Преобразуем выражение:
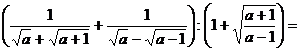
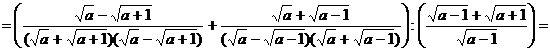
 ; но при условии a > 1; |a| = a,
; но при условии a > 1; |a| = a,
|a - 1| = a - 1; тогда 
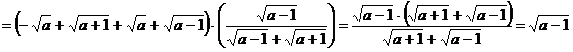 .
.
Ответ:  , при a > 1.
, при a > 1.
2. Решить уравнение: 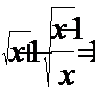
Решение
1-й способ
Найдем область допустимых значений переменной:

 Решим эту систему, используя метод интервалов (см. рис. 41):
Решим эту систему, используя метод интервалов (см. рис. 41):
Рис. 41
В результате получаем  .
.
Рассматривая уравнение на этом множестве, преобразуем его:
 .
.
Возведем обе части полученного уравнения в квадрат, получим

 .
.
 не входит в область допустимых значений и не является корнем данного уравнения.
не входит в область допустимых значений и не является корнем данного уравнения.
Ответ:  .
.
2-й способ
Положим  , тогда
, тогда  .
.
Получим систему уравнений из которой исключим x.
 Положим
Положим  .
.
Второе уравнение получим, заменяя в первоначальном уравнении, квадратные корни их значениями:  .
.
Получим систему уравнений:
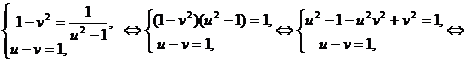
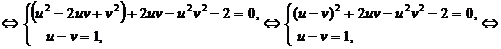


Решим первое уравнение системы:
 .
. 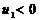 не удовлетворяет условию
не удовлетворяет условию  и является посторонним корнем. Остается второй корень. Делаем обратную подстановку и находим значение x.
и является посторонним корнем. Остается второй корень. Делаем обратную подстановку и находим значение x.
 .
.
Ответ:  .
.
3. Найти область определения функции:  .
.
Решение
Выражение, находящееся под знаком квадратного корня должно быть неотрицательным:  .
.
Выражение, находящееся под знаком логарифма должно быть положительным. Но поскольку оно находится под знаком модуля, то достаточно потребовать, чтобы оно не равнялось нулю  . Кроме того, логарифм находится в знаменателе дроби, а значит не может равняться нулю, тогда
. Кроме того, логарифм находится в знаменателе дроби, а значит не может равняться нулю, тогда  .
.
Получим систему неравенств:

 Решим неравенства методом промежутков (см. рис. 42):
Решим неравенства методом промежутков (см. рис. 42):
Рис. 42
В результате, находим область определения функции  .
.
Ответ:  .
.
4. Решить уравнение:  .
.
Решение
Область допустимых значений переменной:  или
или  .
.
Преобразуем уравнение: 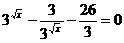 . Положим
. Положим  , тогда получим алгебраическое (квадратное) уравнение:
, тогда получим алгебраическое (квадратное) уравнение: 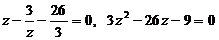 ,
,
 .
.  не удовлетворяет условию
не удовлетворяет условию  и является посторонним корнем. Получим уравнение
и является посторонним корнем. Получим уравнение  .
.
Проверка
 ,
,  .
.
Ответ:  .
.
5. Решить уравнение:  .
.
Решение
Преобразуем уравнение. Для этого возведем в квадрат двучлены, получим:



 ;
;
 - это уравнение однородное первой степени относительно
- это уравнение однородное первой степени относительно  и
и  ,
,  .
.
Разделим обе части этого уравнения на  , получим:
, получим:
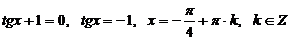 .
.
Ответ:  ;
;  .
.
6. Отношение оснований равнобедренной трапеции равно m. Найти отношение радиусов окружностей, описанной около трапеции и вписанной в нее.
Решение
Рассмотрим вписанную окружность

Рис. 43
1. Пусть ABCD данная трапеция, у которой AD = BC - по условию.
Обозначим большее (нижнее) основание трапеции AB = a, меньшее (верхнее) основание CD = b, по условию  (см. рис. 44).
(см. рис. 44).
Центр вписанной окружности находится в точке O, лежащей на высоте KN, соединяющей середины оснований трапеции и делит ее пополам OK = ON.
2. AN = AE = a/2 - как отрезки касательных, выходящих из одной точки.
По этой же причине BN = BF = a/2, DE = DK = b/2.
3. Из  по теореме Пифагора
по теореме Пифагора  , где DP = 2r,
, где DP = 2r,
 .
.
Подставляя значения, получим:  .
.
Зная, что  , выразим a и подставим в полученное выражение, найдем:
, выразим a и подставим в полученное выражение, найдем:
 .
.
Рассмотрим описанную окружность

Рис. 44
1. Рассмотрим  . Из него, по теореме синусов, имеем
. Из него, по теореме синусов, имеем  .
.
2. В  , где r - радиус вписанной окружности. Отсюда,
, где r - радиус вписанной окружности. Отсюда,  .
.
3. Из  , по теореме Пифагора,
, по теореме Пифагора,  , но
, но  , а
, а
 , тогда получим
, тогда получим
 .
.
4. Из формулы  найдем R:
найдем R:
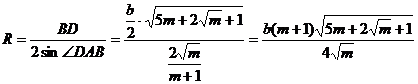 .
.
5. Найдем отношение радиусов окружностей
 .
.
Ответ:  .
.
7. Определить размеры открытого бассейна объемом 32м3 с квадратным дном, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение
1. Так как дно бассейна - квадрат, то можно предположить, что бассейн имеет форму прямоугольного параллелепипеда ABCDA1B1C1D1, изображенного на рисунке 45.
Обозначим сторону его основания a, высоту - H, она же является длиной бокового ребра.
Тогда его объем будет равен  .
.

Рис. 45
2. Для облицовки стен и дна, необходимо знать площадь боковой поверхности и площадь основания, т. е. искомая площадь будет равна:
 .
.
3. Из формулы объема выразим H и подставим в формулу искомой площади:
 .
.
4. Рассмотрим S, как функцию от a, при a > 0 и исследуем эту функцию на минимум, т. е. найдем значения a из промежутка a > 0, при которых эта функция принимает наименьшее значение.
Для этого найдем производную и критические точки:
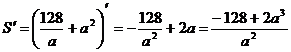 .
.
Критические точки: 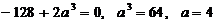 .
.
Итак, исследуем функцию в точке 4.
При  , значит, функция, на этом промежутке, убывает.
, значит, функция, на этом промежутке, убывает.
При 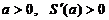 , значит, функция возрастает.
, значит, функция возрастает.
В точке a = 4 функция имеет минимум, т. е. на облицовку бассейна пойдет наименьшее количество материала.
Высота бассейна будет равна:  м.
м.
Ответ: сторона основания должна быть равна a = 4 м, а высота H = 2 м.
Вариант 12
1. Упростить выражение:

2. Решить аналитически и графически уравнение:

3. Решить уравнение: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Два велосипедиста выехали одновременно из одного пункта в одном направлении. Первый из них ехал со скоростью 15 км/ч, а второй - со скоростью 12км/ч. Спустя полчаса из того же пункта в том же направлении выехал третий велосипедист, который через некоторое время догнал второго, а еще через 1 час 30 мин. догнал и первого. Найти скорость третьего велосипедиста.
7. Найти радиус основания r и высоту h прямого кругового конуса, вписанного в шар радиуса R так, чтобы его объем был наибольшим.
Решения
1. Упростить выражение:
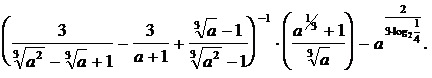
Решение
Область допустимых значений переменной a:  .
.




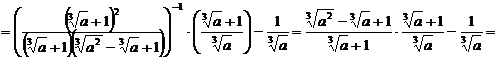
 .
.
Ответ:  .
.
2. Решить аналитически и графически уравнение:

Решение
Аналитическое решение
Данное уравнение равносильно совокупности двух смешанных систем:
(1)  и (2)
и (2) 






